このシリーズでは、東大に引き続き、平成の京大理系数学の問題を1年ずつ遡って解いていきます。
京大の数学の問題も、難易度は高いですが良問の宝庫であり、演習価値が非常に高いです。
(時々、どうしようもなく難易度が高く、筆者の力量でも解けない問題が出てくることがありますが、どうかご容赦くださいm(_ _)m )
12回目の今回は、2008年の問題です。
2007~2010年の問題は、甲セットと乙セットの2種類がありますが、より難易度が高く受験者人口が大半を占めていた乙セットを解きます。
第1問

直線と対数関数が交点を持たない条件を求める問題です。
このタイプの問題は、「直接方程式を解く」「定数分離して、グラフと横棒の交わりを調べる」という解き方が典型的ですが、今回は、その2つともがうまくいきません。
xとlogxの混じった方程式は直接解くことができませんし、定数分離をしようにも2文字以上あるのでうまくいかないわけです。
よって、最後の手段。f(x)=px+q - logxとしたときに、f(x) = 0が実数解を持たない条件を調べましょう。(この実数解が、2曲線の交点になりますので。。)
f'(x)=p-1/xとなるので、pの正負によって場合分けが生じます。
pが0以下の時は、f'(x)は常にマイナスになるのでf(x)は単調減少となり、f(x)でx→±∞してあげれば、f(x)はあらゆる値をとりうることが分かります。当然0にもなりうるわけです。よって、このときはf(x)=0は必ず実数解を持ちます。
一方、pが正のときは、f(x)は極小値を持ち、この極小値が常にプラスならf(x)は常にプラスになりますので、実数解を持たないことになります。
<筆者の解答>

第2問

n秒間にA,B,C,Dのすべてを通過する確率を求める問題です。
まずn=1, 2のときに確率が0になるのは明らかですので、nが3以上のケースを考えます。
この問題は、「一度も通過しない頂点がある確率」という余事象を考えるとやりやすいです。
このもとで、
・2頂点しか通過しない場合
・3頂点しか通過しない場合
を重複なく数えましょう。
対称性から、「AとBしか通過しない場合」、「Dだけ通過しない場合」を考えれば十分です。
<筆者の解答>

第3問

空間図形に関する証明問題です。京大特有の抽象的な設定の出題ですね。
問題文を分かりやすく言い換えてあげると、
「4つの直線のそれぞれに対して、うまくA,B,C,Dを選んであげると四角形ABCDが平行四辺形になる」ことを証明せよ、となります。
よって、平行四辺形になるような頂点A,B,C,Dを、4つの直線がどんな配置であってもとってこれることを証明します。
まず、4つの直線をla, lb, lc, ldとして、それぞれの単位方向ベクトルをea, eb, ec, edとしましょう。
このとき、3次元空間を考えていて、ea, eb, ec, edのどの3つ同一平面上にいないので、この4つのベクトルのうち3つが一次独立になります。よって、ea, eb, ecが1次独立だとすると、edが、ea, eb, ecを使って、
ed = p×ea + q×eb + r×ecと表現できます。ここで、p, q, rは、4つの直線の配置によって決まる数で、A,B,C,Dの取り方とは関係なく決まります。
一方で、OA = a×ea, OB = b×eb, OC = c×ec, OD = d×ed という形でA,B,C,Dをとってきます。このa,b,c,dの値をうまいこと選んであげると平行四辺形になることを言いたいわけです。
ここで、平行四辺形になる時、ABベクトルとDCベクトルが一致するので、
a=dp, b=-dq, c=dr という関係式が求まります。p,q,rは予め決まっている数なので、
適当にdを決めてあげて、a,b,cを、
「aはpをd倍した数、bはqを-d倍した数、cはrをd倍した数」 となるように選んであげればよいことになります。
ここまでの考察で、4つの直線の配置によらず、A, B, C, Dをうまいこと選んでくれば平行四辺形を作れることが証明できました。
<筆者の解答>

第4問

絶対値付きの2つの2次関数の交点の個数を数える問題です。これは難問です。
絶対値のついた問題は、絶対値を外すのが基本ですが、この問題の場合、一見すると絶対値の外し方が4通りもあり、手に負えなくなってしまうように見えます。
ここで、今回考えるべきものは、方程式|x^2-2| = |2x^2 + ax -1|の解の個数です。この方程式の両辺を|x^2-2| で割り算してしまえば、絶対値を一か所にまとめることができるので、実質場合分けを2通りで考えればよくなります。
よって、割り算できないx^2 = 2のときのみを例外扱いして、それ以外では、この割り算した状態で絶対を外してみましょう。
まず、x^2 = 2のケースを調べると、|a|=3/√2となるので、aがこの値の時は少なくとも1個は解を持ちます。
残りは、絶対を外して処理してあげると、元の方程式は
「x^2+ax+1 =0 または 3x^2 +ax-3 =0」と変形できます。ここで「または」であることに注意です。
この2つの2次方程式の解の個数の和が求める答えになりますが、愚直に「軸の位置が・・・」などと場合分けするのは大変です。何せ方程式が2つもあり、2つの方程式の解のダブり具合なども考慮しないといけないですから。
ここは、お馴染みの定数分離を使って、2つの方程式を2つのグラフに読み替えて図に起こしてしまったほうが賢いです。一目瞭然で解の個数が分かりますね。
(この点、分数関数の微分が使える理系でも難問なのに、それが使えない文系の人にとっては捨て問なんて生易しいレベルではなくなりますね。。)
この2つのグラフと、横棒との交点の個数を数えてあげればよいです。
最後に、最初に例外扱いした|a|=3/√2の場合も加えて終了です。
<筆者の解答>

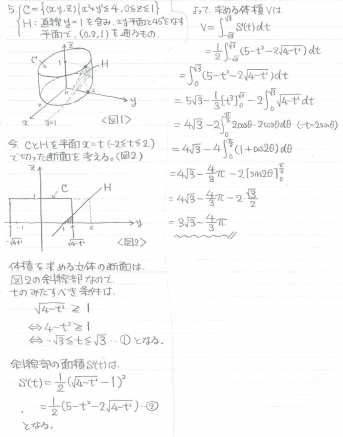
第5問

(筆者注:誤0<x<1 正0<z<1)
円柱を平面で切った時の片方の立体の体積を計算する問題です。
座標軸に垂直な平面で切って断面積を求めて積分するというお馴染みの流れです。
今回は、Hの断面が常に変わらない上に、円柱の断面が長方形となって扱いやすくように、x=tで切ると見通しが良いです。
<筆者の解答>
第6問

(筆者注:誤 同一経度、正 同一緯度)
地球上の2点を結ぶ2通りの航路の長さを比較する問題です。大分実用的な設定の問題ですね。
最初に言葉の確認ですが、「緯度」は、北極を北緯90°、赤道を北緯0°とした南北の位置を決める尺度であり、「経度」は、イギリスのグリニッジ天文台を東経0°とする東西の位置を決める尺度です。
今回の問題の場合、「経度」の定義はあまり影響を受けませんが、「緯度」の定義は致命的に影響します。赤道を誤って「北緯90°」としてしまうと、経路の長さが全く変わってしまいます。
よくシベリアなどの寒い地域を「高緯度地域」、サハラ砂漠みたいな暑い地域を「低緯度地域」と言ったりします。このことから赤道は「北緯0°」と連想したいですね。普段からニュースなどに触れて常識力を養っておくとよいと思います。
ここまで社会のお勉強でした。本題に戻りましょう。
まずは、地球の半径をRとして、地球の中心を原点とする座標系を定義します。軸の方向は、xy平面が赤道、z軸方向を北極のある方向とします。x軸は東経0°とします。
このとき、東経α°、北緯β°となる点の座標は、
(Rcosβcosα, Rcosβsinα, Rsinβ) とかけることが図形的に分かりますので、これによりAとBの座標が求まります。
次にR1, R2をそれぞれ考えます。
R1は同一緯度を飛び続けるのですから、半径R/2の円周上を60°ぐるりと回った経路になります。
R2は、地球の大円に沿って移動するのですから、半径Rの円周上を角度θだけぐるりと回った経路になります。θは、OAベクトルとOBベクトルのなす角です。
あとは、両者の比をとってあげましょう。その際は、角度の単位を揃えてあげないといけません。三角関数表や電卓は通常、「度」で定義されているので、「度」に揃えるとよいです。
この問題から分かる通り、同一緯度で飛ぶよりも、地球に大円に沿って飛んだほうが距離を節約することができます。
この「大円に沿った経路」が、球面上における最短距離になることが一般的に知られています。よって、飛行機は燃料と時間の節約のために、常に大円に沿うように航路を決めて運行されています。
よくメルカトル図法の地図(いわゆる普通の平面の地図)の上で、飛行機の動きが直線ではなくカーブで表現されるのはこれが理由ですね。
ちなみに、地図で調べてみたら、
東経75° 北緯60° →カザフスタンの北側らへんのロシア領土
東経135° 北緯60° →ハバロフスク(ロシアの極東)
という感じでした。ほぼロシア国内旅行ですね。こんなに広いなんて、なんておそロシア笑
<筆者の解答>
