東大京大に引き続き、他の旧帝大の問題も取り上げていきます。この記事では、九州大学の1989年の問題を取り上げます。最終回です。
第1問
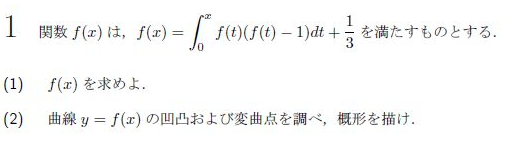
積分方程式の問題です。
(1)x=0を代入して初期条件を、xで自分することで微分方程式ができるのでそれを解きます。
(2)f''(x)の増減を調べましょう。
<筆者の解答>

第2問

三角関数と行列の融合問題です。
(1) f(x)を、倍角の公式を使って1次式に直してあげれば最大値・最小値が求まります。これが、問題文にある方程式の解と一致するかを確認します。
(2)A^2 =Aとなる条件を求めていきます。AがIの定数倍になる場合とならない場合で、場合分けが発生します。
<筆者の解答>

第3問

4本の三角関数で囲まれた面積を求める問題です。
(1)cosとsinが混じっていて、かつ角度が違っていると処理が難しいので、どちらかを揃えましょう。今回の場合は、sinに揃えると考えやすいです。和積公式を使って、積の形にして考えます。
(2) (1)の結果を使うと4曲線の交点のx座標が求まりますので、図を丁寧に書いて、面積計算しましょう。
<筆者の解答>


第4問

確率分布に関する問題です。期待値と標準偏差の比を考察します。
(1)m枚中k枚が表になる確率を計算し、定義通りに期待値と分散を計算します。分散は、V(X) = E(X^2) - { E(X) }^2 で計算されます。
(2) f(a)= (a^2 +1) / (1+a)^2として、f(a)の取りうる値を調べれば十分です。
<筆者の解答>

第5問

ジョギングメニューを題材にした場合の数の問題です。
(1)fnに関する漸化式を作ります。
fn-2にコースBかCを追加する、fn-1にコースAを追加する でfnを構成できます。
こうしてできた漸化式を使って、題意を証明しましょう。
(2) (1)を使ってfnの一般項を求めます。
(3)問題文の通りに素直に計算しましょう。
<筆者の解答>
