文系数学の最難関、一橋大学の2019年の問題を取り上げます。
第1問

整数問題です。
a3を計算してみると、平方数になるか判断できない式が登場するので、a3が平方数になるとしたときに、a4以降が平方数になるかどうかを調べましょう。
<筆者の解答>

第2問

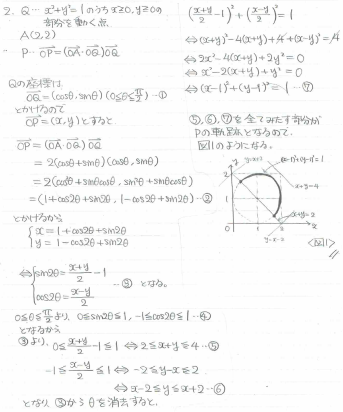
軌跡の問題です。
定石通りQを(cosθ,sinθ)とおいて、与式を計算してθを消去しましょう。x,y座標の取りうる値のチェックを忘れずに。
[訂正]最後の円の方程式の導出の場面にミスがあり、正しくは半径√2です。
<筆者の解答>
第3問

3次関数の接線と面積の問題です。
(1)Pにおける接線の式からQが求まり、x=tにおける接線がQを通る条件からtを求めましょう。
(2)図に描いて、テンプレ通りに積分計算です。
<筆者の解答>

第4問

円に内接する円に関する問題です。
円の接する条件から、C3の中心座標と半径の関係式を作っていきます。
<筆者の解答>

第5問

ビンゴゲームのような題材の確率問題です。
(1) S=3 は、1列に3つ全て並ぶ場合です。
(2)S=1となるのは、2個だけ1直線に並ぶ場合です。このとき、2つの場所を決めると、残り1つの入れる場所は大分限られてきます。
(3)S=2を素直に計算するよりも、S=0の場合を計算して、全体からS=3の確率、S=1の確率、S=0の確率を引いてしまったほうが早いでしょう。
※答案の最後の最後で初歩的な計算ミスをしてしまってました。正しくは3/7です。申し訳ありませんでした。
<筆者の解答>
