理系数学の最難関の一角、東京工業大学の2019年の問題を取り上げます。
第1問

三角形の辺と面積の不等式を証明する問題で、誘導なしの問題が数学オリンピックの過去問に出ていたと話題になった問題です。とはいえ、難問ばかりのこのセットの中では最も易しい問題なので、解いておきたい問題です。
(1) ノーヒントだとかなりの難問(それこそ数オリに出題されるレベル)になっていたはずですが、座標が設定されているのでこれをヒントにすれば比較的簡単に解くことができます。p, q, r, Sを全てh,s,tの式で表して、平方完成することを考えます。式を書いてみるとhだけ仲間外れなので、まずhから平方完成するとよいでしょう。等号成立条件は、直感的には見え見えですよね。
(2) (1)ができていればサービス問題です。四面体の4つの面全部に対して(1)の不等式を立ててあげればよいです。
<筆者の解答>

第2問

積分方程式の問題で、見た目の厳つさに違わず計算が長く大変な難問です。
この問題は、DIOにたどり着くまでに何人ものスタンド使いを倒していった条太郎一行のように、いくつもの強敵を倒さないと攻略できません。
まず最初に目につくのが、積分区間の厳つさ(1/x~2/xなんていう分数が入っている)と、積分の中身にあるf(xy)という関数。基本的に関数の中に2つ文字が入っている状態はよろしくないので、1文字にすることを考えます。答案ではt=xy と変換しています。積分の計算においてはxはただの定数なので、これによってyの積分をtの積分に変えることができます。と同時に、積分区間も1~2とすっきりした形になり一石二鳥です。これで第1関門突破です。
次に気になるのが、積分の中にある絶対値の存在。tがxより大きいか小さいかが要になるので、積分区間をxを境目に区切って絶対値を外す必要があります。すると、∫f(t)dtと∫f(t)logt dt という実質2種類の積分形しか登場しない形にできます。分数として1/xがあると面倒なだけなので、両辺にxをかけて少しでも計算しやすい形にしておきます。ここまでが第2関門。
ここからは、両辺をxで微分して・・という積分方程式のお馴染みの解法になります。微分すると同時にx=1,2を代入したときの式も作るとよいでしょう。とはいえ、この過程においても∫t(logt)^2 dtといった積分の計算が要求されますし、非常に難度が高いです。
最終的に出てくる答えもきれいではないので、正直この問題は時間が余ったら挑戦するぐらいの優先度で良い気がしますね。。
<筆者の解答>


第3問

複素数を使った格子点の数え上げ問題です。
問題文が分かりにくく、z/(3+2i)のままでは考えにくいです。そこで、複素平面上でzが格子点になっているという設定を使い、zの個数を数える問題に読み替えてあげるのが、この問題の最大のポイントです。
このあと、便宜上w=z/(3+2i)とします。
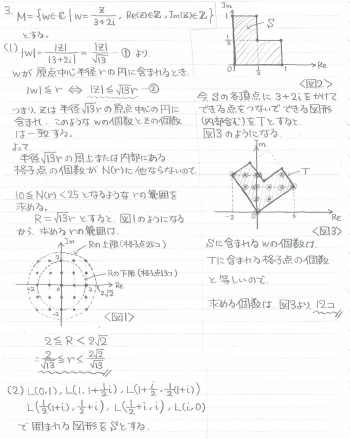
(1) wが原点中心の半径rの円の中にあるというのは、|w|≦rと数式で言い換えられます。
|w| = |z|/√13となっているので、 |z|≦√13 r と条件を言い換えることができます。結局、この問題は、
「原点中心で半径√13 r の円の中に含まれる格子点の数が10以上25未満になるrの範囲を求めよ」
と翻訳できます。ここまでくれば考えやすくなるでしょう。実際に図を描いて円の中に納まる格子点の数を数えてしまえばよいです。
(2) この小問もzの世界の言葉に置き換えてあげるとよいです。
問題文にある線分を繋いでできる図形をSとします。ここで、「複素数の掛け算= 回転と縮尺変化」という事実を使ってS全体に3+2iをかけてあげると、Sを原点の周りに回転させ縮尺を変化させた新しい図形Tが出来上がります。これでzの世界に落とし込むことができました。
結局、この問題も「Tの中に含まれる格子点の個数を求めよ」と翻訳することができますので、図を丁寧に描いて格子点を数えましょう。高々10個程度なので、下手に代数処理するよりも手で直接数えたほうが遥かに楽です。
<筆者の解答>
第4問


空間にn枚の平面を配置したときに何個の領域に分けられるかを考察する問題で、2019年に現れたレジェンド級の超難問です。私自身、初見では全く手も足も出ませんでした。。
見た目通りに試験問題として全く機能していない問題なので、即捨て安定です。
この問題に関しては、私が色々書き連ねるよりも、動画による解説がいくつか挙がっているのでそちらを見てもらったほうが良いです。特にyoutuberの環耀さんの動画が、非常に空間図形の図が分かりやすくオススメです。(1)~(3)でそれぞれ動画化しており、合計1時間半にも及ぶ超大作の解説動画になってます(下に動画を張っておきます)。
とはいえ、何もコメントなしなのは癪なので、少しばかり書いておきます。
(1) 「n本の直線で、平面を最大いくつに分けられるか」は、俗に「怠けた仕出し屋数列」と呼ばれています。今回は、その3次元バージョンになります。2枚、3枚と実験してみると、新しく追加した平面とそれまでに配置した平面との交線によって分けられた領域の数(=「怠けた仕出し屋数列」)だけ、空間の領域数が増えることが分かります。これを利用して、漸化式を立てて求めることができます。この答えをTnと置きます。
(2) 2番目に大きい領域数の候補はTn -1 なので、この状況が作れるかどうかを確かめます。領域を減らすには、「交線を平行にして交点を消す」か「交点を1個に集中して領域をつぶす」かの2通りの方法があります。
(3)3番目に大きい領域数の候補はTn -2 なので、同じようにこの状況が作れるかを確かめるのですが、なんとn=4の場合「だけ」Tn -2のケースが作れず、Tn -3となってしまいます。これを試験場で気づけというのは無茶な相談でしょうに。。。
↓以下、環耀さんの動画です。
(1)
(2)
(3)
ということで、以下の答案も上記の動画を参考にして自分なりに書いてみたものとなっており厳密性に欠けた粗だらけな代物になってしまっていること、ご了承ください。
<筆者の解答>



第5問

数列の最大値を求める問題です。
近年稀にみる奇問だった第4問とは打って変わり、非常にやり応えのある美しい良問です。本番では第1問とこれ(あわよくば第3問も)が解けていれば十分だったと思います。
(1)一見数列とは無関係な関数の増減を調べる問題です。まぁ、当然(2)のヒントなのですが。微分して増減を調べるのですが、今回は2階微分まで計算しないと増減が見えてきません。
(2)bkは、階乗や指数など掛け算の要素だけでできた数列になっています。こんな数列の最大最小を調べる方法は、「前後で比を取る」の一択です。約分でどんどん消えていくのでスッキリした式にできます。
今回の場合は、こうして比を取った式に対数を取ってあげると、(1)のf(x)が登場することになります!!この伏線回収が、実に巧妙で美しいのがこの問題のポイントです。
(1)で証明した事実を使ってあげると、bk/bk-1 と1との大小関係がどうなっているかを調べることができ、結果bkの増減が分かることになります。
<筆者の解答>
