今日行われた2022年度共通テストの問題を見ていきます。
まずは数学IAを扱います。
※試験当日に解いており、ミスがあるかもしれません。
<略解>

[1/17追記]採点の結果、第2問[2]のス、ソ~チでミスがありました。
スの正解は③、ソ~チの正解は0.63です。申し訳ありませんでした。
<個別解説>
第1問 [1]

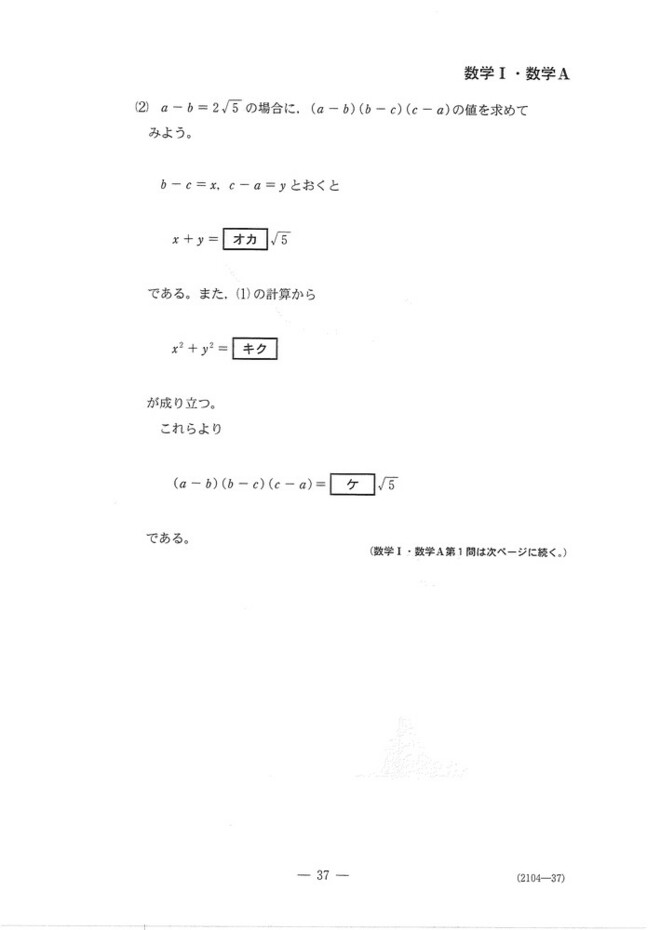

2次式をひたすら処理していく問題です。
(1)アイ:問題文に書いてある通り(a+b+c)^2を展開すれば一発です。
ウエ:こちらも左辺を展開すれば今までの情報から値が求まります。
(2) オカ:こちらもx+yをa~cの式に直せば容易です。
キク:ウエの結果を利用すればよいでしょう。
ケ:これまでの情報からxyを求めましょう。(x+y)^2 = x^2 +2xy +y^2を使えばOKです。
<筆者の回答>

第1問 [2]
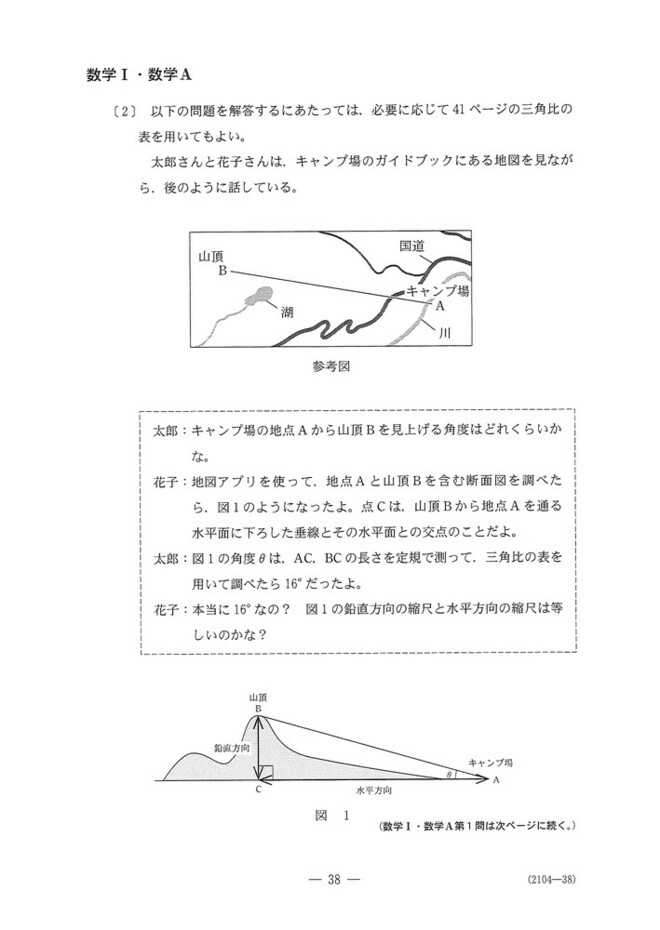

仰角を評価する問題です。
図1でAC=a, BC=bとすると、tan16°=b/aです。ところが縮尺分図1は実際の長さよりも短くなっているので、仰角はAC=100000a, BC=25000bと縮尺分を修正した実際の長さで計算しないといけません。すると、tan∠BAC=tan16°/4と求まります。
<筆者の回答>

第1問 [3]
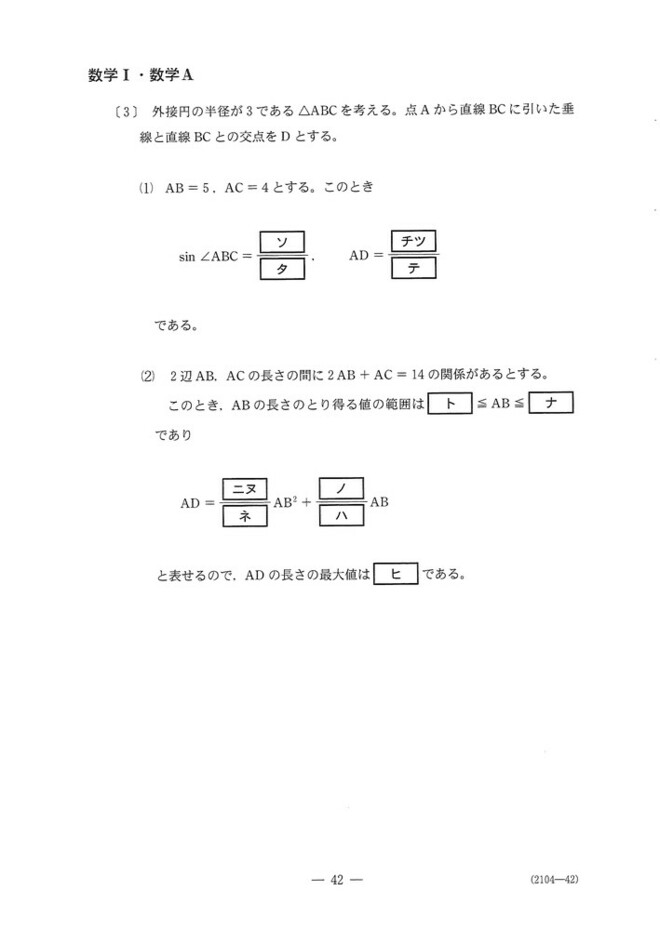
三角比の計算問題です。
(1)正弦定理とsinの定義を利用します。
(2)やや難しい問題です。
正弦定理を使ってAB, ACをsinのしきで表現して、問題文の関係式に代入してしまいましょう。このとき、0<sin∠ABC≦1を利用して、sin∠ABCの範囲を決めることができます。
ADについては、問題文の関係式と、sinの定義を利用してあげるとABの2次関数で書けます。ここから最大値を求めるのですが、平方完成すると軸の位置がト~ナの外側にくることに注意しましょう。
<筆者の回答>

第2問 [1]


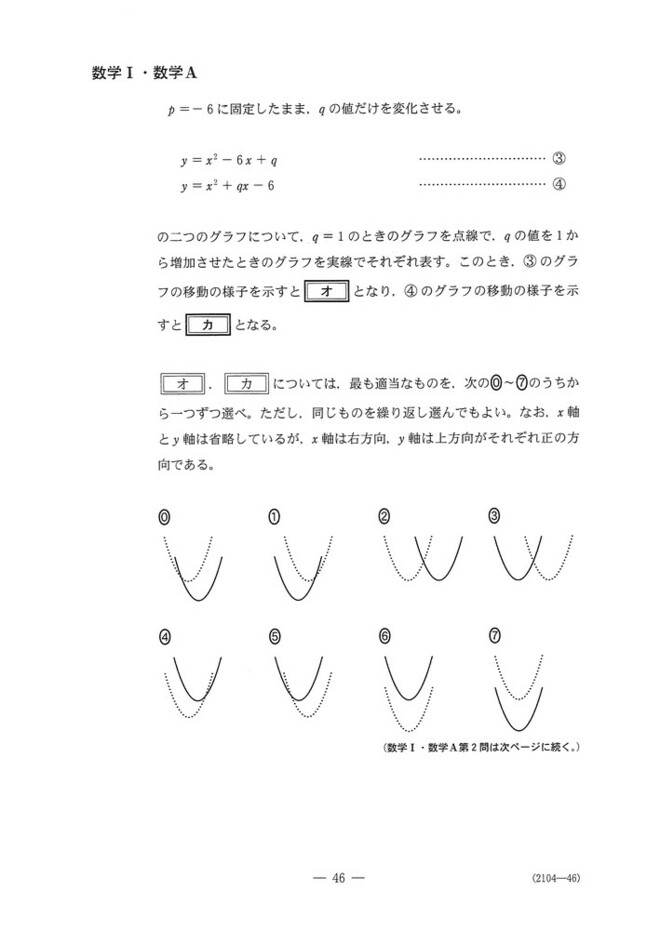

2本の2次方程式の解の個数と、放物線の動き方を考える問題です。
この問題、前半はなんと京大2008年理系第4問の焼き直しのような設定になっています。ということで難易度は共通テストとしては高い部類です。
(1)これは代入して、逐一方程式を解けばよいでしょう。
(2) n=3になるのは大きく2パターンあります。
1つは、問題文の会話にある通り、共通の解があるとき。もう1つは、片方が重解を持つときです。この後者を思いつけたかがカギですね。
前者については、p=qは不適なので、α=1とすぐに求まります。そこからqが求まります。
後者については、①②のどっちが重解を持つかで場合分けして検討します。
(3) qを大きくすると、③はy軸正方向に平行移動しますし、④は平方完成するとy軸負方向かつx軸負方向に平行移動することが分かります。
(4)Aの不等式と、Bの不等式を解いて重なりがあるかを見ます。Aの上限が3以上、Bの下限が負なのは一目瞭然なので、Aの下限とBの上限が気になります。ウ<q<エの範囲で、両者の取りうる値を調べてあげれば、両者がダブる瞬間がないことが分かり、AとBに重なりがないことが分かります。
<筆者の回答>


第2問 [2]


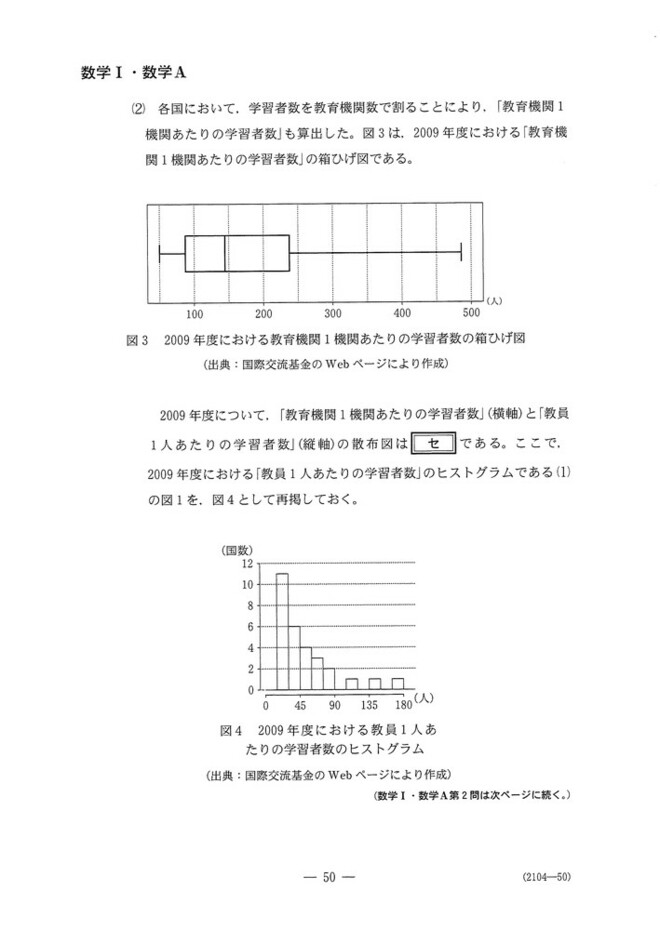
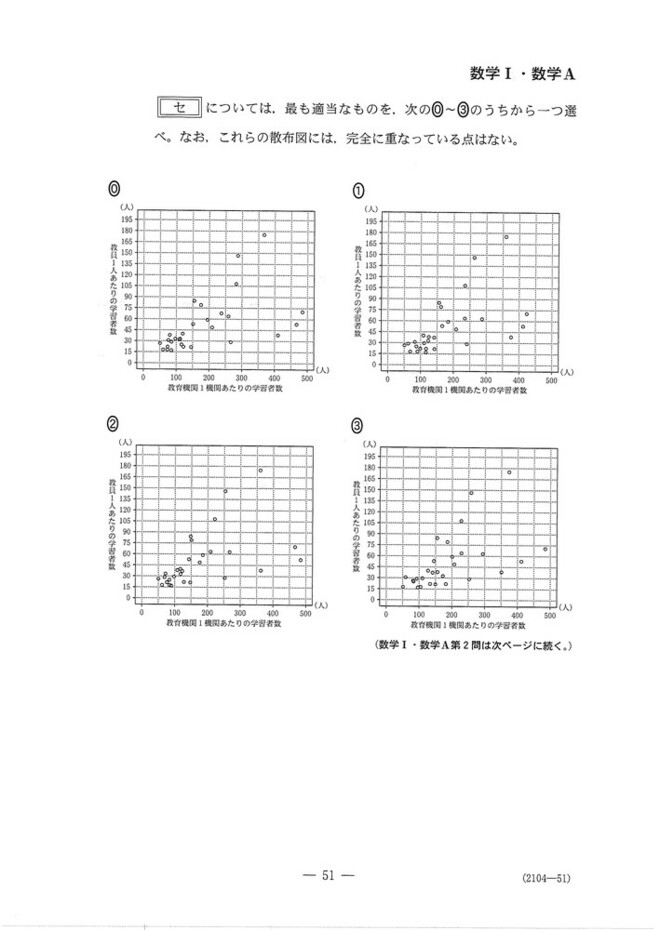

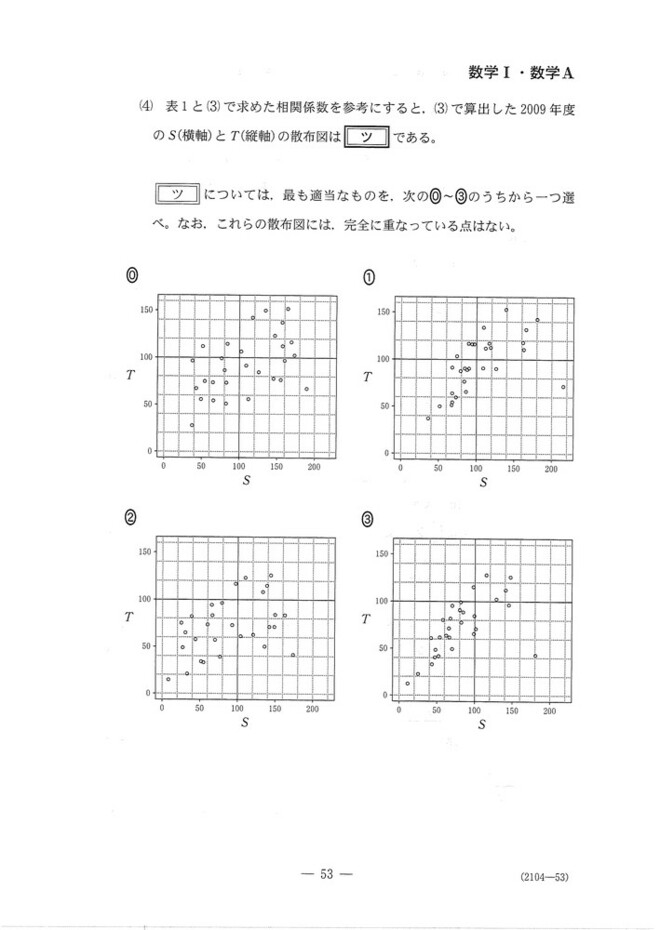
データの読み取り問題です。
(1)まずはヒストグラムに書かれている縦軸の数字を左から書いていくとよいでしょう。縦軸の合計が両者とも29になるので、中央値は14.5, 第1四分位は7.25, 第3四分位は21.75とわかります。累計がそれらの値になるような横軸の階級値を比較すればよいでしょう。
(2)箱ひげ線図から最小値が50付近、最大値が450~500となります。この時点で最大値が小さすぎる①は候補から外せます。あとは第1四分位が90~100、第3四分位が250付近となることから②だけがOKだとわかります。
(4)SとTの平均値が100付近にある0と①はNGだとわかります。
あとは相関係数が比較的大きい事から②かな?と思いました。この小問はあまり自信がありません。
<筆者の回答>


※[1/17追記] (3)で数値の書き写しをミスるという凡ミスをやらかし、相関係数の結果がずれてしまいました。
第3問


確率の問題です。
(1)2人の場合は、配り方は2通りしかないですね。3人の場合は、配り方は全部で6通りあり、そのうち全員が他人のプレゼントをもらうのは2通りだと、書き下せばわかります。
(iii)については、一回で終わる確率が1/3, 終わらない確率が2/3なので、1,2,3,4回で終わる確率をそれぞれ計算して合計しましょう。
(2)
サ:Aさんだけ自分のプレゼントをもらってB~Dさんが他人のプレゼントをもらう場合の数を数えます。こうすると実は(1)の結果が利用できることに気が付きます。あとは自分のプレゼントを受け取る1人の選び方が4通りあることから、この結果に4をかければOKです。
シ:考え方はサと一緒で、今度は自分のプレゼントをもらう2人を固定して考えます。
スセ:ちょうど3人が自分と同じプレゼントをもらう状況はありえないので、あとは全員が自分のプレゼントをもらう場合を考えればOKです。
(3) (2)と考え方は一緒です。場合の数を数えるときに(2)までの結果が使えることに気付くと楽になります。
(4) A~Eの全員が他人のプレゼントをもらう場合の数と、Eだけ自分のでA~Dが他人のプレゼントをもらう場合の数を計算しましょう。
<筆者の回答>


第4問


整数問題です。
(1) 問題文にあるヒントを使うと、5^4 = 2^4m+1とおけるので、2^4×(整数)+x=1とできます。xは2^4で割ると1余る数なので、x=1, 17・・・と続いていきます。
(2)5^4 = 2^4m+1を2乗すればよいです。
(3)問題文の誘導に従って考えてあげると、5^5x - 625^2 =10^5の倍数となるので、こうなるxが求まります。
(4) (3)と同じ考え方で解いていけますが、yの計算が非常に面倒なので、試験場では捨てても仕方ないかなと思います。
<筆者の回答>

第5問
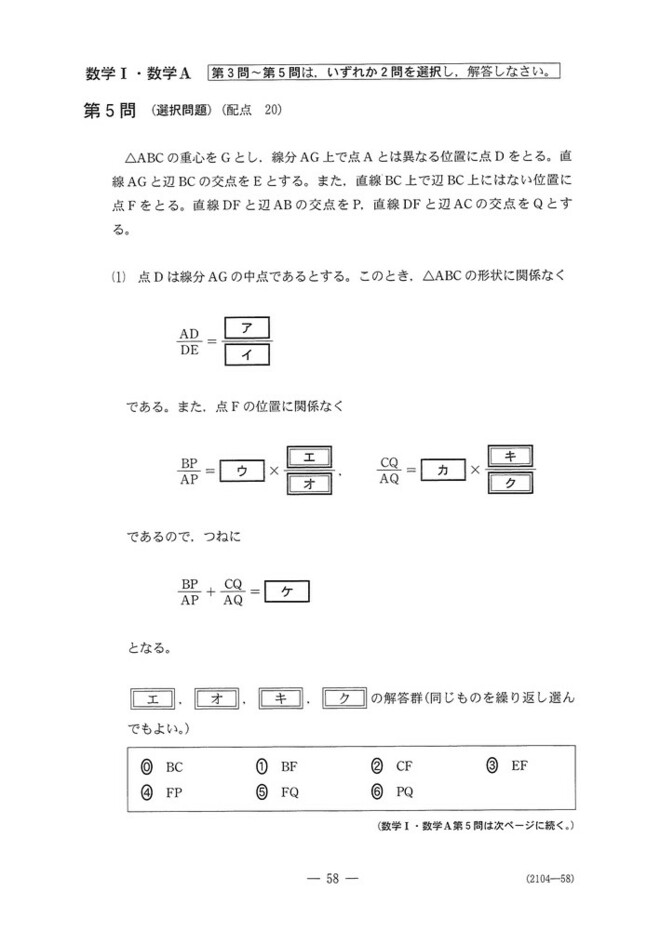
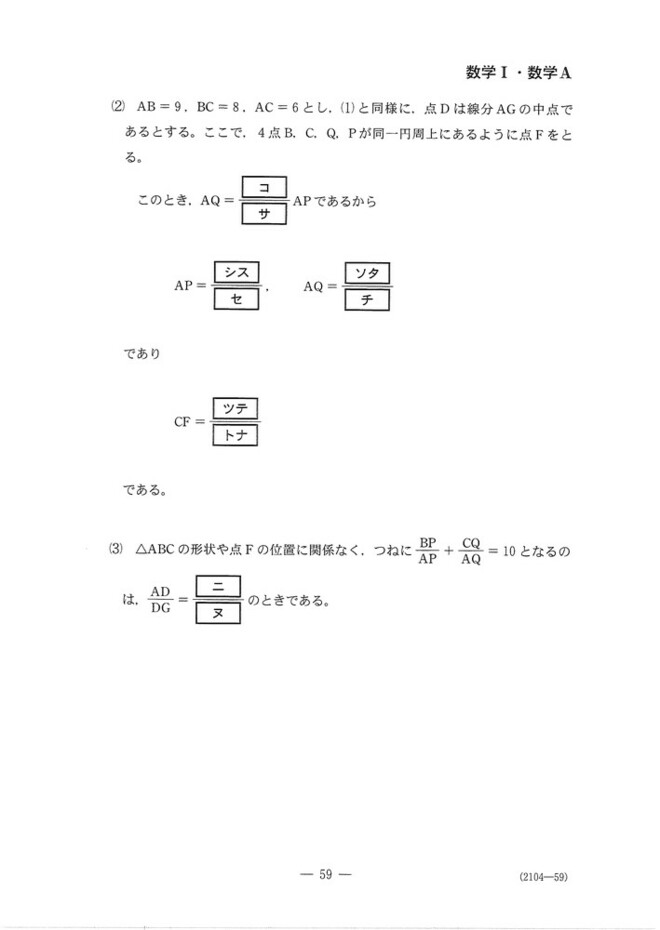
初等幾何の問題です。
(1)アイ:重心の性質、AG:GD=2:1を利用します。
ウ~ク:メネラウスの定理を2回使いますが、AG,GDが入るように使うとよいでしょう。
ケ:BE=ECを利用すると、一定値になることが分かります。
(2) コサ:同一円周上にある⇔方べきの定理が成り立つ、と言い換えられます。
シ~チ:コサとケの式を利用すれば求まります。
ツ~テ:さらにウ~クを利用すれば求まります。
(3) AD: DE=t:(1-t)とおいて、(2)までと同様にして考えていきtを求めましょう。
<筆者の回答>

