このシリーズでは、平成の東京工業大学の後期日程の数学の問題を解いていきます。
10回目の今回は2002年です。
第1問
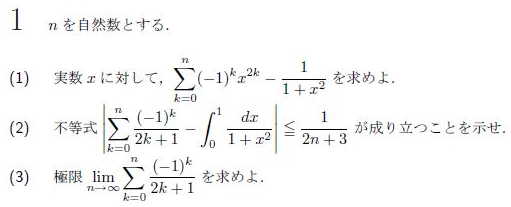
(1)シグマの部分は初項1, 公比-x^2の等比級数になっているので直に計算することができます。
(2) (1)の結果を使って与式の左辺を計算していきます。(1)の結果から、積分の中身を書き換えることができ、計算を進めるとうまい具合にシグマの部分が消えてくれます。結局、与式の左辺=「x^(2n+2)/(1+x^2)の0~1での積分値」となります。
与式の右辺が1/(2n+3)となっていて、これは分子のx^(2n+2)を積分することで出てきそうな数です。そう思うと、積分の中身の分母1/(1+x^2)が邪魔に感じてきます。0≦x≦1では、1/(1+x^2)≦1と評価できるので、これで邪魔な分母を消すことができます。
(3) (2)の式ではさみうちの定理を使えば、求める無限級数は、∫dx/(1+x^2)に収束することが分かります。この積分はx=tanθと変換するとうまくいくタイプの積分ですね。
最終的に出てきた答えをまとめると、
1-1/3+1/5-1/7+・・・・=π/4
となり、つまり、「奇数の逆数を足したり引いたりを繰り返した数がπ/4になる」、という結果になります。この無限級数の事を「ライプニッツ級数」と呼びます。
バーゼル問題と同じように、単純な分数を足したり引いたりしているだけなのに、最終結果に円周率πが登場するという不思議な結果になります。
ここから円周率πの近似値を計算できそうですが、この級数は収束のスピードが非常に遅い(結構な項を足さないとπ/4に近づかない)ので、こうした近似計算には残念ながら不向きな級数です。
<筆者の解答>

第2問

空間内の道のりの最小値を求める問題です。
(1)話をxy平面だけに限定すれば、Qを通る2本のCの接線の情報から視覚的にMの存在範囲が分かります。
(2) P~Mの道のりをL1, M~Qの道のりをL2とし、L=L1+L2とします。
L2は直線なので容易に計算できますが、問題はL1の方です。L1はSの側面上の最短距離なので、Sの側面の展開図から計算する必要があります。
こうしてLがθの式で求まったので微分して検討します。
θのまま微分するとルートも交じってて非常に複雑な式になってしまうので、t=2cosθ/2と変換してtで微分すると少しは計算が楽になります。tの範囲は(1)の結果からわかるので、あとは頑張って計算するのみです。
<筆者の解答>

