このシリーズでは、名古屋大学の後期の数学の問題を解いていきます。
初回の今回は2007年です。
第1問

グラフの図示の問題です。
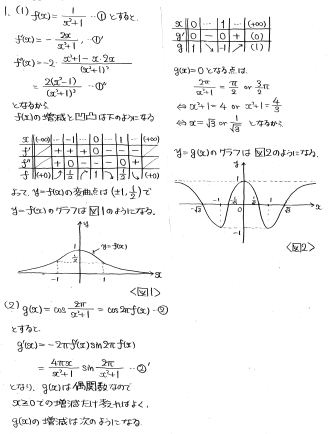
(1)これは教科書レベルでしょう。y''まで計算して凹凸も調べていきます。
(2)微分して符号を調べればよいでしょう。流石に変曲点の情報までは不要だと思います。
<筆者の解答>
第2問

1次変換に関する問題です。
(1) Pkが楕円上にあると仮定してPk+1が楕円上にあることを証明するという、帰納法でよいでしょう。
(2) t=1としたときの行列をAとすると、ケーリーハミルトンの定理からA^2=A-Eが求まります。これを使ってAの累乗を計算していくと、A^6=Eとなることが分かります。
(3)要するに、「tをうまい事調整すれば、Pnはどんな周期にもできる」ということが証明したい命題なので、周期がMになるようなtをうまいこと見つけてくればOKということになります。
(2)と同じような「ケーリーハミルトン→A^M=EとなるMを探す」という手段だとうまくいかないので、別の方法を考えたい所です。こうなれば、(1)の結果をうまく使いたいですね。
C=√(2-t)/(2+t)としてあげると、(1)の結果からPn(cosθn, Csinθn)の形に描くことができます。問題文の漸化式からθnの一般項をtの式で求めることができます。
ここで、Pn+M=Pnとなるなら、θn+M - θn が2πの整数倍であればよいわけです。今回はtが一個でも見つかればいいのでθn+M - θn =2πとしてあげればよく、するとtがMの式でバシッと決まります。
<筆者の解答>



第3問

論証問題です。
問題設定が抽象的で分かりにくいですが、「〇〇できる」という内容の証明には数学的帰納法が非常に適しているので、これを使っていきます。
n=1のときは成立が自明で、n=2のときも4点がどんな配置でもOKだと分かります。
そうしてから、n=k, k+1での成立を仮定して、n=k+2の時に成立することを証明するという流れになります。
既存の2(k+1)個の点群に新しくP,Qという2点を加えるのですが、このP,Qの配置の仕方で場合分けが発生するので、適宜線分を付け替えたりして証明していきましょう。
(答案でも、ひょっとしたら抜け漏れがあるかもしれません・・・)
<筆者の解答>

