このシリーズでは、東京医科歯科大学の数学の問題を解いていきます。
7回目の今回は2016年です。
第1問

約数の和に関する整数問題です。背景には「完全数」があると思われます。
名状しがたい希少な数 ~完全数~ - ちょぴん先生の数学部屋 (hatenablog.com)
(1) S(n)=2n⇔(1+p+p^2)(1+q)=2p^2*qとなるので、pとqが互いに素なことを利用すると、1+qが2p^2の倍数だと分かります(1+p+p^2は必ず奇数なので、1+qが偶数となります)。これを手掛かりにして解いていきます。
この小問で求めているS(n)=2nを満たすnのことを完全数と呼びます。
(2)S(n)=n+1という関係式は、nの約数の和がn+1→nの約数は1とnしかない、ということを意味しているので、この関係式を満たすnは素数です。
ということで、この問題は「n=2^a -1が素数なら、aも素数である」を証明する問題となります。これは直接証明するのが難しいので、対偶を取って「aが合成数なら、n=2^a -1も合成数である」を証明するとよいでしょう。
2^a -1の形になる自然数を「メルセンヌ数」と呼び、その中で素数になっているものを「メルセンヌ素数」と呼びます。
ちなみに、この問題の逆「aが素数なら、n=2^a -1も素数である」は必ずしも成り立ちません(a=11の場合が反例の一つ)。
(3)一般に互いに素な自然数A,Bに対して、S(AB)=S(A)S(B)となることを使うと、S(n)=(2^a -1)×S(2^a -1)となり、S(n)≦2nのとき、S(2^a -1)≦2^aとなります。
もし2^a -1が合成数だと、S(2^a -1)は必ず2^aよりも大きくなるので不適です。ということで、2^a -1は素数で確定します。そして(2)で証明した通り、その時aは素数となります。
aが素数なら、2を除けばaは奇数です。2^mの1の位がどうなっているかを調べれば、aが奇数の時にnの1の位が6か8になっていることを示せばよいと分かります。a=2は別個にn=6と調べてしまえばよいでしょう。
<筆者の解答>


第2問

(訂正:r3の条件は、「または」ではなく「かつ」)
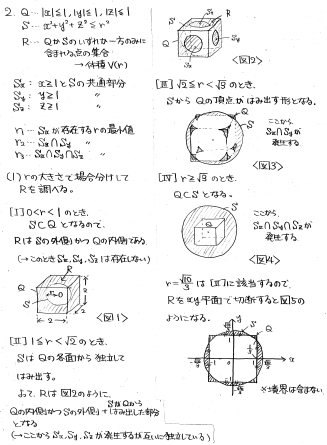
立方体と球の重なりを考える問題です。問題文は非常にややこしく見えますが、図に落としていくと見かけほど難しくありません。
(1)rの大きさによって先に場合分けをしてしまいましょう。
0<r<1なら、球Sが立方体Qの中に完全に収まります。1≦r<√2のときは、Qの6つの面から少しずつSがはみ出しますが、お互いに独立してて重なりがありません。√2≦r<√3のときは、はみ出しが融合するようになって、むしろSからQの頂点だけが少し顔を出すような状態になります。r≧√3では、QがSの中にすっぽり納まります。
こうして場合分けすると、r=√10/3は2番目の1≦r<√2の場合に該当します。
(2)事前に場合分けしておいたおかげでr1~r3がすぐに分かり、V(r1)はQ-Sで、V(r3)はS-Qでシンプルに計算できます。
(3)Sxの体積は、回転体の体積の考え方で計算できます。対称性からSyとSzの体積もSxと同じになります。
(4) r=1を境に場合分けが発生します。r<1ではV(r)が単調増加なのは自明なので、メインは1≦r≦√2での考察です。(3)の結果からV(r)を計算して微分すればよいでしょう。
<筆者の解答>

第3問

特殊な関数を題材とした積分の計算問題です。
(1) <<u>>の値は、uが正の時はu自身、uが負の時は0となるので、xの値で場合分けしてf(x)の正体を探っていきましょう。
(2) 積分の中身がf(x-t)という扱いにくい形になっているので、τ=x-tと変数変換してあげるとよいでしょう。あとはxの値で場合分けして(1)の結果を使って積分を計算していきましょう。
(3) a=∫g(x)dx, b=∫xg(x)dx, c=∫x^2*g(x)dxと定数でおいてしまえば、平方完成でp(s)の最小値は、s=b/aでc-b^2/aと計算できます。
ということで、あとはa~cを計算するのみですが、結構面倒です。
<筆者の解答>


