みなさん、こんにちは。
今回から、量子力学の基礎方程式「シュレディンガー方程式」について、いくつか代表例を解いてみる、というネタを紹介しようと思います。
今回は初回なので、そもそも「シュレディンガー方程式」とは何か?という導入部分から解説し、最も簡単かつ量子力学のエッセンスが凝縮された「井戸型ポテンシャル」について紹介します。
今回紹介する「井戸型ポテンシャル」には「無限の深さの場合」と「有限の深さの場合」の2パターンがあり、両方紹介すると長くなってしまうので前後編に分け、今回は前編として「無限の深さの場合」について紹介します。
0.導入
量子力学とは、原子や電子といったミクロな粒子を対象にした物理学の事です。
長い間、ニュートン力学とマクスウェル方程式(古典電磁気学)で全ての現象が説明できると信じられてきましたが、次第にこれらでは説明のつかない現象が次々に発見されていきました。
それらを説明するために発明された理論こそが「量子力学」で、その基本となる方程式が、今回紹介する「シュレディンガー方程式」です。
0-1. シュレディンガー方程式
百聞は一見に如かず。まずはシュレディンガー方程式がどういう方程式かを見せます。

色々と意味不明な記号があると思うので説明していくと、次のような感じです。
h:プランク定数 →量子力学で頻出する物理定数で、エネルギー×時間の次元を持ちます。プランク定数 - Wikipedia
m : 考えている粒子の質量
∇^2 : ラプラシアン
ベクトル解析 カテゴリーの記事一覧 - ちょぴん先生の数学部屋 (hatenablog.com)
V : 粒子が受けている力のポテンシャルエネルギー
Ψ:波動関数(後述)
i : 虚数単位
つまり大雑把に言って、
という形の方程式になっていて、右辺には虚数のiが登場しています。これは、量子力学が「虚数」の存在なしには論じられない理論だということを意味しています。
さて、ここまでの量で一番意味不明なのが、主役であるはずの関数、波動関数Ψですね。
波動関数というのは、大雑把に言えば「粒子の存在確率」や「粒子の状態」を表す関数です。(※正確には、|Ψ|^2が、確率を表します)
存在「確率」という記述に疑問を感じると思います。ここが、量子力学独特の不思議な考え方なのですが、
「粒子がある時刻でどの場所にいてどういった速さで動いているかは『確率的』にしかわからない(不確定性原理)」
というのが量子力学の大原則なのです。
初期条件を入れれば時刻tで物体がどこにいてどんな速度で運動してるかを正確に調べられたニュートン力学とは全然違う世界なのです。
ということで、シュレディンガー方程式は、粒子の「存在確率」「状態」を表す波動関数Ψを求めるための方程式となります。
0-2. 時間に依存しないシュレディンガー方程式
本来、上記のようにシュレディンガー方程式は「時間微分」と「空間微分」の両方が混じった方程式です。しかし、実際にはこの2種類の微分を切り分けて考えることができます。
まず、以下のように波動関数Ψを、位置に関する関数ψと時間に関する関数Tの積に分けてしまいます。

これを元の方程式に代入して全体をΨで割ると、

このように左辺は位置だけの関数に、右辺は時間だけの関数にできます。
かたや位置だけの関数で、もう一方は時間だけの関数で、その双方がイコールで結ばれています。この辻褄を合わせる手段は1つだけです。両方ともがただの定数であればいいわけです。
この定数をEとすれば、次のように方程式を分割できることが分かります。

こうして空間微分の式と時間微分の式を切り分けることができました。この手法の事を「変数分離」と呼び、シュレディンガー方程式を解く上での常套手段です。
まず、時間微分の方程式(C)の方を見ていくと、これは非常に簡単な微分方程式で、結果が指数関数になるタイプです。

指数関数の肩に虚数単位iが入っているので、オイラーの公式から本質的には三角関数、つまり時間経過に伴って振動する関数になることが分かります。
(オイラーの公式に関してはこの記事を参照ください。数学界のKingとQueenは、愛で結ばれた・・~世界で一番美しい数式、オイラーの等式~ - ちょぴん先生の数学部屋 (hatenablog.com) )
この時間依存性は、元々の方程式のV(ポテンシャルエネルギー)、つまり粒子の置かれている状況によらずに成立する話なので、これからの議論の話題にはあまりなってきません。本題はむしろ空間微分の式(B)の方です。
(B)を変形してできる下のような方程式

を、「時間に依存しないシュレディンガー方程式」と呼び、以降「シュレディンガー方程式を解く」と言えばこの方程式を解くことを指すことにします。
0-3. 方程式の構造
この「時間に依存しないシュレディンガー方程式」はどういう方程式なのか解説していきます。

まず左辺は、波動関数ψにラプラシアンを含んだ空間微分の演算子がかかった形をしています。この演算子の事をまとめて「ハミルトニアン」と呼びます(Hと表記することが多いです)。一方の右辺は、波動関数ψに定数Eがかかっている形になっています。
この形、どっかで見たことないですか?線形代数で習う「固有値・固有ベクトル」の話と酷似しているのです。
この2次曲線の正体はな~んだ? ~行列の対角化~ - ちょぴん先生の数学部屋 (hatenablog.com)

行列Aをベクトルにかけると、基本的には大きさも向きも変わってしまいます。しかし、ある特定の方向のベクトルxに対しては向きが変わらないという性質がありました。この特別なベクトルの事を「固有ベクトル」、結果として出てくる定数を「固有値」と呼ぶんでした。
これを今回の話に置き換えてみます。

演算子Hを関数にかけると、基本的には関数の形が変わってしまいます。しかし、ある特定の関数ψに対しては定数倍以外に形が変わらないという性質があります。この特別な関数の事を「固有関数」、結果として出てくる定数を「固有値」と呼びます。
そして、今回扱う演算子であるハミルトニアンはエネルギーの次元を持つ演算子なので、右辺の定数Eもエネルギーの次元を持ち「固有エネルギー」と呼ばれます。
つまり、「ハミルトニアンを波動関数にかけることで、粒子の持つエネルギーEが求まる」というのが、シュレディンガー方程式の意味する所であり、
シュレディンガー方程式を解くという作業は、ハミルトニアンHの固有関数ψと、対応する固有エネルギーEを求める作業と同じなのです。
1. 井戸型ポテンシャル(無限深さ)
シュレディンガー方程式として、最もシンプルな状況である「井戸型ポテンシャル」を考えます。
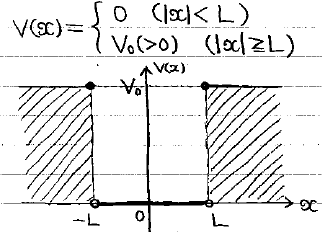
井戸型ポテンシャルというのは、下の図のように-L<x<LではV=0で、その外側ではV=V0となるポテンシャルエネルギーV(x)のことで、簡単に言えば、「両側に壁がある空間に粒子が閉じ込められてる状況」となります。
今回の記事では、その中でもV0=+∞となる「絶対に壁の外に出られない」状況について、粒子の固有エネルギーと波動関数を調べていきます。
1-1. 一般解の導出
解くべきシュレディンガー方程式は下のようになります。今回はx軸上だけで考えるので、ラプラシアンはx微分のみ残します。
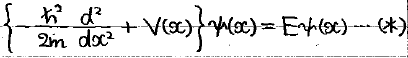
外側ではVが+∞なので粒子は存在できません。よって、そこでの波動関数は0です。
![]()
あとは内側について考えればよいですね。
内側の微分方程式は、三角関数を解に持つパターンなので以下のように一般解を求めることができます。

1-2. 境界条件
このままだと、任意定数が2つ残ったままになってしまいます。なので、これらが決まるように境界条件を課します。
考える境界条件は以下の2つです。
1. x=±Lで波動関数は連続である
2. 波動関数の2乗(=粒子の存在確率)の総和は1
外側で波動関数は0だったのですから、連続となるにはx=±Lで波動関数が0になっていればOKです。この条件を考えると、以下のようになります。

sinとcosは同時に0にならないので、この条件からAとBのどちらか一方が0にならないといけません。なので、どっちの値が0になるかで場合分けを行います。
先にcosだけが生き残る場合を見ます。
このとき、coskL=0となることから、kLの値に制限がかかります。

kは固有エネルギーEの関数でしたから、自動的に固有エネルギーEに制限がかかります。

確率の総和=1については、波動関数の2乗を積分した値が1になればよいです。

よって、波動関数と固有エネルギーは以下のように整数nを用いて表せます。

sinだけ生き残る場合も全く同様です。

以上の結果をまとめると、波動関数と固有エネルギーは以下のようにまとめられます。

1-3. 結果から言えること
この結果から言える重要な知見を見ていきましょう。
波動関数と固有エネルギーは整数Nを用いて表せました。これは「固有エネルギーは、連続的ではなく飛び飛び(=離散的)になる」ということを意味します!
このように、粒子のエネルギーが飛び飛びの値を取るというのが量子力学に特有な重要な性質です。この現象を「エネルギーの量子化」と呼びます。
各固有エネルギーに対して粒子の波動関数を図示すると下のようになります。

このようにエネルギーが大きくなるほど節の数が多くなることが分かりますね。
次回の記事では、壁の外側が無限大ではなく「有限の高さ」になった場合について考えていきます。