皆さん、こんにちは。
今回からいよいよ「数値解析」シリーズの最終目標、「有限要素法」について紹介していきます。
大きく次の3回に分けてupする予定ですが、
・構造解析
・周波数応答解析
今回は一番最初のベースになる「構造解析」の概要をお話ししたいと思います。
1. 有限要素法のコンセプト
コンピュータによる数値解析を用いて製品の設計検討を行うことを、一般的にCAE(Computer Aided Engineering)と呼びます。今回から紹介する「有限要素法」は、CAEの中でも最もメジャーな数値解析の手法です。
ある物理現象を解明したければ、その現象の従う微分方程式を解くことになります。しかしこれまで解説してきた通り、コンピュータは直接微分方程式を解くことはできず、何かしら離散化を施して近似計算する必要がありました。
常微分方程式を数値解析で解く ~オイラー法・ホイン法・ルンゲクッタ法~ - ちょぴん先生の数学部屋 (hatenablog.com)
偏微分方程式の数値解析&陽解法と陰解法の比較 ~熱伝導方程式を題材に~ - ちょぴん先生の数学部屋 (hatenablog.com)
また、現実に取り扱う製品は形状が非常に複雑であり、方程式を実際に手で組み上げ手で解くことなど不可能なわけです。
そこでどうするか。
有限要素法のコンセプトは、
製品を細かい単純なメッシュに分割
→各々のメッシュについて方程式を立てる
→それらの方程式を全体で連立して解く
というものです。
例えば、下の図のように、引張強度試験片を、一方を壁に固定しもう一方を力Fで引っ張る状況を考えます(奥行方向の厚みは十分薄いものとします)。
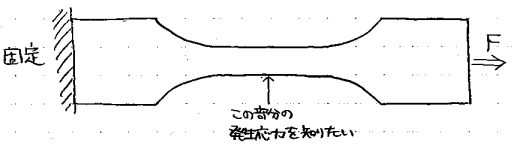
この時、最も応力が集中するのが中間部の凹んだ部分なのでそこの応力値を求めたいわけですが、このままだとうまく解けません。そこで、下の図のように試験片を三角形または四角形の「メッシュ」に分割します。

この三角形、四角形の1つ1つを「要素(element)」と呼び、各要素の頂点を「節点(node)」と呼びます。
この各節点に対して方程式を立てそれを全節点に渡って連立して解いてあげれば、最終的に各部分の応力を求めることができます。
メッシュが細かければ細かいほど、形状の再現性が上がり、より細かく応力を調べることができるので精度向上が期待できます。が、その分節点が増え、解くべき方程式の本数が増えてしまうので解くのに時間がかかります。
このように計算精度と計算時間がトレードオフの関係になることに注意が必要で、如何に要求される精度と現実的な計算時間を両立できるようにするかが、CAEエンジニアの腕の見せ所です。
2. 変位と力を求めていく流れ
今回は話を単純化するために三角形要素の場合に絞って説明したいと思います(四角形要素も考え方は同じです)。
2-1. 単一要素の場合
まずは、要素が1つだけの場合について説明します。
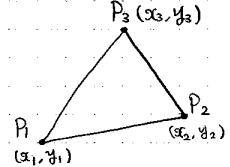
三角形要素の各節点をP1, P2, P3とし、各節点の元の座標を(xi, yi)とします。
これらの接点が外力
![]()
を受けることで変位
![]()
が発生するとします。
さらに、要素内部(節点以外の部分)の変位は、その点の座標(x,y)の1次式で補間近似できるものとします。
![]()
(※このように内部を1次式で近似する要素を「1次要素」といいます。要素によっては2次式で近似するものもあり、それは「2次要素」と呼ばれます。今回は簡単のために1次要素だという前提で話を進めます)
このとき、変位と力の間には次のような関係式が成り立ちます。

要はフックの法則の行列版という感じの式で、剛性方程式と呼ばれます。。ばね乗数に相当する左辺の係数行列を剛性マトリクスと呼びます(このマトリクスの導出については後述)。
有限要素法の分野では、しばしばベクトルを{ }で、行列を[ ]と略記して書きます。今回の②は次のように略記することが多いです。
![]()
②は結局のところ連立1次方程式であり、これを解いてしまえば未知の変位や力が求まることになります。
この②が全ての基本となる式です。
2-2. 複数要素
実際の解析においては1要素で解くなんて場面はなくて、複数の要素の集合体を取り扱うことになります。
今回は簡単のために、三角形要素が2つ繋がった構造体について考えていきます。

左側の三角形要素を[1]、右側の三角形要素を[2]とし、上の図のように[1]の1節点が固定されていて、[2]の1節点がx方向に外力Fを受けている状況を考えます。
このとき、各節点の変位は、固定されているP1だけが既知で、残りは未知数です。
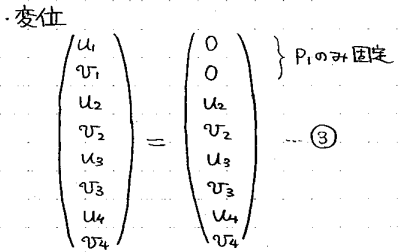
外力は、実際に力を加えているP4が既知で、外力を受けていないP2, P3は0, 反力を受けるP1のものだけが未知となります。

さて、要素[1], 要素[2]のそれぞれについて、②のような剛性方程式を立ててみましょう。
剛性マトリクスがそれぞれ6×6の行列になって煩雑なので、下のように簡略化して書いてしまいます。


この2つの剛性方程式は、節点P2, P3がダブっているため独立ではありません。そのため、この2つを合体させる必要があります。
合体は、各々の剛性マトリクスを下のように合体させれば事足ります。

要は、ダブってる部分だけ対角方向にずらして足し算し、成分が元々なかった部分は0で埋めてあげます。このようにしてできる系全体の剛性マトリクスは全体剛性マトリクスと呼ばれ、[K]と書かれることが多いです。
![]()
これで、大元になる剛性方程式が出来上がりました。
そこに、③と④で調べた境界条件を反映させます。

破線で囲った部分が未知数です。
ここで、連立1次方程式を解く際は、左辺のベクトルに未知数を固め、右辺のベクトルには既知の値を入れた状態で解くのが普通なのですが、⑧では左辺と右辺の両方に未知数と既知の値が入り乱れていて考えづらいです。
そこで、既知の値と未知数が綺麗に分かれるように、⑧’のように行列を分割します。

実線で囲った行列・ベクトルは既知の値のみ、破線で囲ったベクトルは未知数のみで構成されています。
⑧’を分解した式の形で書けば次のようになります。

こうなれば、⑩を解くことで未知ベクトルUBが求まり、その結果を⑨に代入すればもう一つの未知ベクトルFAが求まりそうです。
というわけで、解くと式の上では次のような形になります。
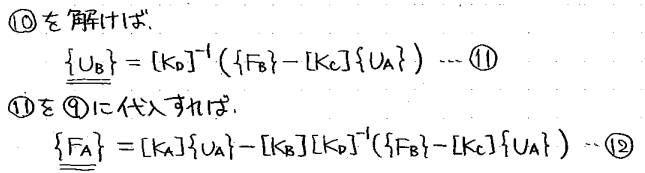
FAはUBを代入するだけで計算できるため計算量は少ないのですが、UBを求める際には連立1次方程式を解くという作業が生じるため、計算量が多くなります。
連立1次方程式の解法の記事でも紹介しましたが、実際に解くにあたっては計算量の多くなる「KDの逆行列計算」ではなく、中学数学的なガウスの消去法が専ら使用されます。
連立一次方程式を解き明かそう ~逆行列・ガウスの消去法・クラメールの公式~ - ちょぴん先生の数学部屋 (hatenablog.com)
いずれにせよ、このような流れで各節点の変位と外力が求まり、そこから最終的に応力やひずみが求まっていくことになります。
3. 剛性マトリクスの求め方
有限要素法ではまず単一要素で剛性マトリクスを組んだのち、それらを合成することで全体剛性マトリクスを作って連立1次方程式を解きました。
では、その元となる単一要素の剛性マトリクスはどうやって組むのか?次はそれについて説明します。
3-1. 応力ひずみマトリクス
まず、材料の持つ特性である「応力ひずみマトリクス」を作ります。
ひずみは変位の座標による微分として、次のように定義されます。

εが軸方向のひずみ、γがいわゆるせん断ひずみと呼ばれる量です。
そして、応力σとひずみの対応関係は⑭のようになります。

物体に力を加えると内部に抵抗力(=応力)が生じて、その力の方向に伸びる一方で、それと垂直方向には縮みますよね。その縮み方を表す比率がポアソン比νです。
そして、応力とひずみの比例係数で、剝離応力(力と同じ向きの応力)に対応するものがヤング率E, せん断応力(力と垂直な向きの応力)に対応するものが横弾性係数Gです。一般に、E=2G(1+ν)の関係があることが知られています。
この⑭はひずみ=の式になっているので、応力=の式に直せば、

となります。⑮の係数行列が「応力ひずみマトリクス」と呼ばれるもので、しばしば[D]と表記されます。
これが剛性マトリクスを構成するための道具の1つです。
3-2. 変位ひずみマトリクス
次に、⑬に基づき、変位とひずみを関係付ける行列「変位ひずみマトリクス」を作ります。
考えている要素が1次要素の場合、要素内部の変位は1次式で補間できるんでした。
![]()
この式における係数を求めることが目標です。
3節点のx変位y変位全てをこの式で表記すれば、

となります。
同じ係数行列が出てきたので、行列式を考えます。

このとき、クラメールの公式連立一次方程式を解き明かそう ~逆行列・ガウスの消去法・クラメールの公式~ - ちょぴん先生の数学部屋 (hatenablog.com)から、x変位uに関する各係数が、
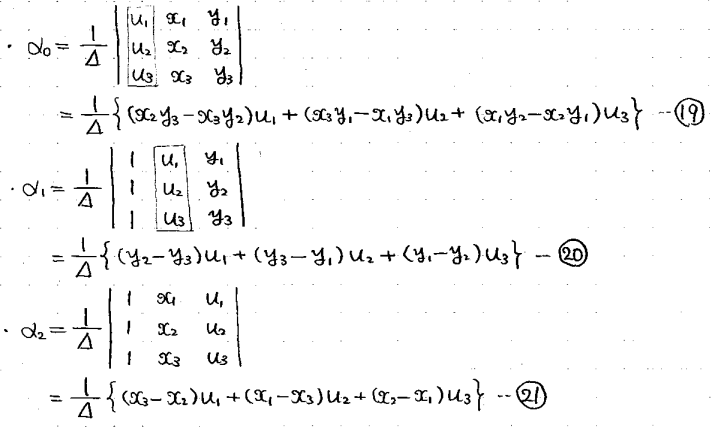
と求まり、行列の形でまとめれば

となります。y変位vの係数も全く同様に

とできます。
これで変位u,vが、座標x,yの式で完全に書けたため、⑬に代入すればひずみが求まります。
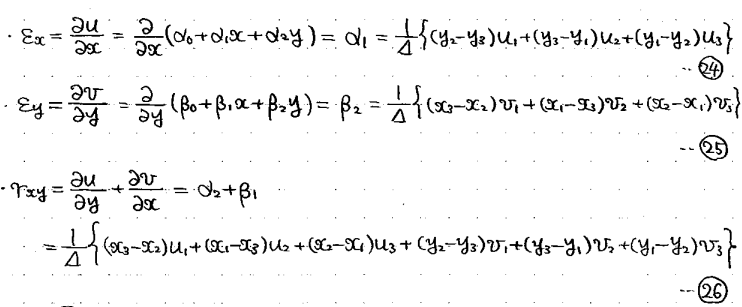
これらを行列の形にまとめれば

となります。この係数行列が「変位ひずみマトリクス」で、しばしば[B]と表記されます。
1次要素の場合は[B]は節点の座標値だけで決まる定数になります。
2次要素の場合は少し過程が複雑にはなりますが[B]を求めていく流れは概ね一緒で、この場合[B]は各成分が座標x,yに依存する1次関数になります。
今回は説明のため導出過程を丁寧に書きましたが、実際の汎用ソフトでは[B]の雛形が予め準備されていて各要素の座標値を代入さえすれば容易に[B]を準備可能です。先述の[D]もヤング率Eとポアソン比νの値を予め与えておけば同様に準備できます。
これが剛性マトリクスを作るための2つめの道具です。
3-3. 仮想仕事の原理
さあ、いよいよここから剛性マトリクスを組み上げていきます。
組み上げるのに必要な法則、「仮想仕事の原理」を紹介しておきましょう。

つり合いの状態にあるとき、中を少し動かしたところでエネルギー変化がない、という法則です。
もっと式にしやすい形で言い換えると、「外力のなす仕事=内力(応力など)のなす仕事」ということです。
これをもとに、外力のなす仕事を左辺に、内力のなす仕事を右辺にまとめると次のような式ができます。

左辺の第1項は、物体表面が受ける大気圧のようなものをイメージすればよく、第2項は重力のようなものをイメージすればOKです。いずれも変位×力を積分してるので、確かに仕事になっています。右辺はひずみによって生じる内部エネルギー(=応力×ひずみの積分)です。
さて、応力計算をするにあたっては重力などの体積力は十分小さく無視できるため、
{F}=0
としてしまいましょう。すると、㉘は、

と変形できます。
1行目⇒2行目では、仮想変位δUは場所に依存しないと見なせるために積分の外に出し、表面力Pの合計が外力fになることを使っています。
以降右辺にはこれまで求めた応力ひずみマトリクス、変位ひずみマトリクスの式を代入し、今回考えた1次要素では[B]が定数行列のため、行列を全て積分の外に出しています。(※2次要素の場合は[B]が1次関数のため積分の中に残り続けることになります。その場合については次々回で触れます)
㉙'では結局外力{f}と変位{u}の比例関係の形になっているため、剛性方程式②'と係数比較すれば、

応力ひずみマトリクス[D]と変位ひずみマトリクス[B]を用いて、無事剛性マトリクス[k]を計算することができました。
4. まとめ
以上から、有限要素法で応力・ひずみを計算していく(構造解析と言います)流れは、次のようにまとめられます。

ヤング率やポアソン比などの材料特性から[D]が、メッシュ形状から[B]が求まり、それらと板厚の情報と合わせて各要素ごとに剛性マトリクス[k]を計算。
全要素に渡って[k]を合成して連立1次方程式を作り、変位{u}と外力{f}で既知の成分の情報(境界条件)を与えて行列を分割し、あとは連立1次方程式をガウスの消去法で解いて、変位{u}と外力{f}を全て確定させ、あとは[B]や[D]と掛け合わせることで、最終的に欲しかった応力{σ}とひずみ{ε}が求まる、
という流れです。
次回は、同じく有限要素法で周波数応答を計算していく流れを解説します。