皆さん、こんにちは。
今回は、賞金の期待値が無限大になる夢のようなギャンブルを取り扱った「サンクトペテルブルグのパラドックス」について紹介します
※記事内で説明しますが、実際にはそんな美味しい話はありませんので、誤解のなきように。
1. サンクトペテルブルグのパラドックス
次のようなギャンブルを考えます。
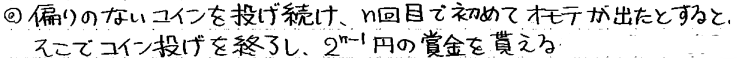
このギャンブルの賞金の期待値Eを求めてみましょう。
n回目に初めて表が出てコイン投げが終了する確率p(n)は、
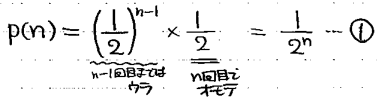
と計算できるので、賞金の期待値Eは、

なんと無限大になってしまいました。
通常ギャンブルは、最初に支払う賭け金と比べて賞金の期待値が大きい、つまり儲かると期待できるときに参加するものです。
翻って今回のギャンブルの賞金の期待値は∞であり、これは賭け金をいくら支払ったとしても儲かると期待できる、美味しすぎるギャンブルだと一見すると思ってしまいます。
ですが、そんな美味しい話はあるのでしょうか?
実際にn=10までの賞金の確率分布を調べると次のようになります。

n=10の値を見ると、512円の賞金を得られる確率すら0.1%にも満たないわけで、実際には仮に賭け金が1000円だったとしても絶対に参加したくないギャンブルなのが実態です。
このように実態として得られそうな賞金と、賞金の期待値Eがかけ離れてしまってる状態が、この問題が「パラドックス」と呼ばれる所以です。
どうして実態と期待値Eがかけ離れてしまっているのか?それはある点を見落としているからです。
2. こんなギャンブルが実際には成立しない現実的な理由
ギャンブルには賞金を振り出す胴元がいるわけですが、胴元と言えど人間、無限に賞金を振り出せるわけではありません。
実際、今回の胴元の資金が10億円だとすると、
![]()
という大小関係から、nが31以上になった時点で賞金が胴元の資金を上回ってしまい支払い不可能になってしまいます。
よって、胴元の資金の都合から、n=30になった時点で強制終了することになります。
この条件の下で期待値Eを計算し直すと、

一転して15円というかなりショボい金額になりました。
これであれば、先の確率分布表からの感覚と大体あってますよね。
というわけで、「胴元の資金を考慮する」というのが、パラドックスを解消する方法の1つになります。
とはいえ、思考実験上は「無限の資金を持つ胴元」という存在を考えることはできるため、そのときの適切な賭け金を提示できなければパラドックスの根本解決にはなりません。
幾多もの数学者が、胴元資金∞の条件下でのこのパラドックスの解消に挑んできたわけですが、今のところ一番いい解消法だろうと考えられている方法を、次に紹介します。
3. 数学的なパラドックスの解消方法 by ウィリアム・フェラー
それは、「1人が1回参加するギャンブルだからパラドックスになってしまった」と考え、「複数人が参加した場合の賞金の平均値の分布を考えたらいいのでは?」というアイデアです。
今、このギャンブルの参加人数をm, m人の賞金の合計をS(m)とします。

m=2^lだとすると、大数の法則から、ある賞金の獲得人数は「総人数m×その賞金を取る確率」で近似することができます。
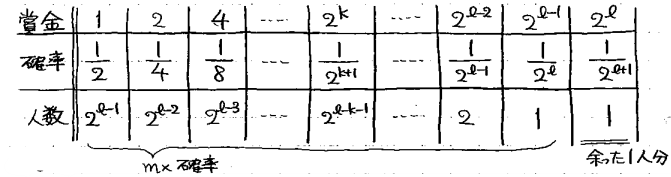
このことから、m人の賞金の平均値は、
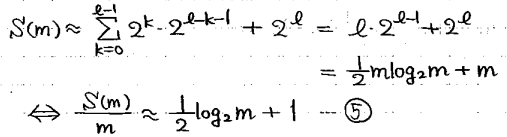
のように、参加人数mの対数で求めることができます。
この平均値を1人あたりの賭け金にしてしまえばいい、というのがウィリアム・フェラーの編み出したアイデアになります。
また、このmは「参加人数」ではなく、「1人が行う回数」と解釈することができ、その場合はトータルの掛金をS(m)にすればいいことになります。

例えば、1000人が1回ずつ行うギャンブルの場合であれば賭け金は1人当たり5.98円、1人が10回行うギャンブルの場合であれば、トータルの賭け金が26.6円となります。
これらは胴元の資金を政変した場合の期待値とあまり大きく変わらず、あまり直感に反さない現実的な賭け金だと言えます。
世の中には美味しい儲け話なんてない。それを改めて肝に銘じましょう。