皆さん、こんにちは。
今回は、ヤコビ法よりも収束性の良い、固有値を計算できる数値解析手法である「QR法」について紹介します。
1. QR分解
1-1. QR分解とは?
最初に、QR法の核になる操作、「QR分解」について説明します。
QR分解とは、①のように、行列Aをユニタリ行列Qと上三角行列Rの積に分解する操作です。(※ただしRの対角成分は全て0以上だとします)
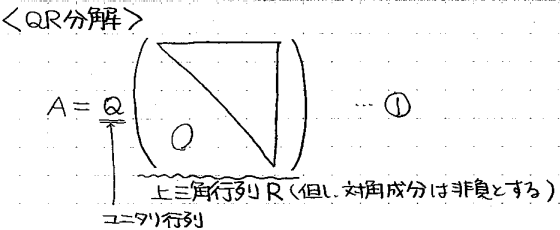
QR分解は、今回紹介する固有値解析だけでなく、色々な場面で多用される汎用性の高い操作です。
例えば、Aの行列式の計算が、上三角行列Rの対角成分の積を計算するだけで済むようになり簡略化されます。

※証明はしませんが、上三角行列Rの行列式はRの対角成分の積になることが知られています。
他にも、Aの逆行列の計算は、実質より計算しやすい上三角行列Rの逆行列を計算するだけで済むようになって簡略化できます。

1-2. QR分解のやり方
では、QR分解を具体的にどうやって実行するのか?最も簡便な方法は、グラム=シュミットの直交化を使う方法です。
1次独立なベクトルたちをキレイな形へ ~グラム=シュミットの直交化~ - ちょぴん先生の数学部屋 (hatenablog.com)
1次独立なベクトルa1~anを正規直交基底b1~bnに変換するグラム=シュミットの直交化の式を再掲すると下のようになります。

この式を全てai=の形に直すと、

となります。
このときに、行列A,Qを次のように定義すると、
![]()
⑤は⑦のように行列の積の形でまとめられます。

右辺の右側の行列がちょうど(対角成分が全て0以上の)上三角行列になるので、これをRとしてあげればOKです。
これでQR分解が完成です。
Pythonで実装すると次のような感じです。

(※グラム=シュミットの直交化のコードはこちらを参照下さい。途中経過のベクトルであるcたちも出力するように改良を施しています。1次独立なベクトルたちをキレイな形へ ~グラム=シュミットの直交化~ - ちょぴん先生の数学部屋 (hatenablog.com) )
他にも、前回のヤコビ法で紹介した「ギブンス回転」固有値問題の数値解析(その2) ~ヤコビ法~ - ちょぴん先生の数学部屋 (hatenablog.com)、後日紹介する「ハウスホルダー変換」を用いてもQR分解を実行することが可能です。
実は、いずれの方法を用いても、QR法の仕方はAが正則であれば一意に定まります。次はその証明を行います。
1-3. QR分解の一意性
n次の正方正則行列Aが、次のように2通りにQR分解できたと仮定します。

この2式から行列Aを消去すると、

(C)から定まる行列Bを定義できます。この行列Bが実は単位行列だと証明できればゴールです。
(C)の左辺に注目すると、Bはユニタリ行列同士の積なのでBもユニタリ行列になります。
(※ユニタリ行列の積がユニタリ行列になることの証明↓)

(C)の中辺に注目すると、Bは上三角行列同士の積なのでBも上三角行列になります。
(※上三角行列同士の積が上三角行列になること、及び上三角行列の逆行列が上三角行列になることの、2×2の場合の証明↓)

よって、Bはユニタリ行列であり上三角行列でもあることが分かり、
ユニタリ行列の性質から、Bの転置行列=Bの逆行列となり
![]()
上三角行列の性質から、Bの逆行列も上三角行列になります。
![]()
これらを総合すると、上三角行列Bは、転置しても上三角行列のままという結論が得られます。これ即ち、Bは対角行列だということになります。
Bがユニタリ行列であることに注意すると、Bの転置とB自身の積は単位行列になります。

よって、Bの対角成分の2乗は全て1となります。
(※今回登場する行列は、全て成分が実数だとしています。)
ここで(C)に立ち返ると、Bは対角成分が0以上の上三角行列同士の積になっていました。

なので、Bの対角成分も全て0以上になります。
故に、Bの対角成分は全て1になり、
![]()
これは即ち、Bは単位行列だということです。
![]()
これが言えてしまえば、もうゴールであり、(C)にこの結果を反映させれば、

AのQR分解の仕方が1通りしかないことが証明できました。
なので、どんな方法を用いてもQR分解の仕方は1通りしかないので、適材適所で手法を使い分けて構わないということになります。
グラム=シュミットの直交化によるQR分解は数値計算だと不安定になりやすいという欠点があるようで、実際の現場では「ギブンス回転」や「ハウスホルダー変換」を使ったQR分解のコードが組み込まれることが多いようです。
ですが、以後登場するコードでは、実装の簡単なグラム=シュミットの直交化でのQR分解を採用させてください。
2. QR法のコンセプト
では、QR法のコンセプトを説明します。

最初の行列をA1とします。
そして、A1をQR分解し、そこで得られたユニタリ行列Qと上三角行列Rを逆の順番でかけたものをA2とします。
以降も同じ操作を繰り返し、Aiが最終的に上三角行列Bになるまで繰り返します。
(※証明はしませんが、この操作の繰り返しによって任意の行列Aが上三角行列Bに収束することが知られています。)
AiからAi+1への変換は、⑨の式から相似変換になっているので前後で固有値は変わりません。
ヤコビ法では相似変換の繰り返しでAを究極の形である「対角行列」まで変換しましたが、QR法では「上三角行列」という少し妥協した形までの相似変換で留めた手法になります。
上三角行列の固有値は、その行列の対角成分そのものになっていることが知られているので、
(※上三角行列の固有値が対角成分になっていることの、2×2の場合での証明↓)

上記で得られた上三角行列Bの対角成分が、そのままAの固有値となります。
QR法のアルゴリズムをPythonで実装すると次のようになります。

試しに、これまで取り上げてきた行列


で実行してみると、
![]()
36回の相似変換で固有値が正しく求まります。
ヤコビ法では同時にAの固有ベクトルも求まりましたが、QR法では相似変換を「上三角行列まで」で妥協した代償として、Aの固有ベクトルはこの手法では求めることができません。
固有ベクトルを知りたければ、求まった固有値の結果をベースに元のAにまで立ち返って別途求める必要があります。
では、固有値が求まった後に、Aの固有ベクトルを求めるにはどうすればよいか?
それには、逆べき乗法の考え方を使えばOKです。固有値問題の数値解析(その1) ~べき乗法~ - ちょぴん先生の数学部屋 (hatenablog.com)
具体的には次のようなアルゴリズムとなります。

逆べき乗法における「Aの逆行列」の部分を、「A-固有値×単位行列E の逆行列」に置き換えたものになります。
あと、注意すべきは、数値解析で求まる固有値は、あくまで近似値であり、真の値に比べて多少なりとも誤差があることです。そのことを強調するために、近似値と真の値を区別して表記しています。
証明は下のように、逆べき乗法の考え方そのものを利用したものになります。

このアルゴリズムをPythonで実装すると下のようになります。

先ほどの例だと、求まった固有値の内「2」が真の値そのものになっていて、このままだと逆べき乗法の段で「分母0」の場面が出てエラーになってしまうため、わざとごくわずかな誤差を加えてエラーを防いでいます。
実際にプログラムを実行すると、

固有ベクトルが正しく求まっています。
4. ウィルキンソンの移動法
ここまでQR法の流れを説明してきましたが、このままだとまだ収束性がよくありません。
なので実際には、収束を速め、より少ない計算回数で済ませるために「ウィルキンソンの移動法」という修正を加えます。
ウィルキンソンの移動法とは、次のように、対角成分を一旦減じてからQR分解をし、逆順で積を計算をしたのちに差し引いた分を戻す、という修正を加えたものです。

この修正をしてもQR法が破綻しない理由は次のようになります。
補正後の行列を
![]()
とおくと、⑮により、

となって、結局Ai+1がAiの相似変換になるので、QR法のコンセプトは破綻しません。
この修正量μは、Aの右下にある2×2行列の固有値(の実部)のうち右下の成分に近いものを選ぶのが主流です。2×2行列であれば固有方程式は2次方程式なので、解の公式で容易に数値計算できます。
3×3行列を例に挙げると次のような感じです。

先ほどのQR法のコードを、ウィルキンソンの移動法を加えて修正したものが下のようになります。

実行すると、
![]()
オリジナルのQR法では36回必要だった相似変換が、22回で済みました。それでいて固有値は正しく計算できています。
5. QR法の実際の流れ
ここで、実際の現場で使用される「QR法」の全体の流れをチャートにします。

まだ説明していない話がいくつか登場していますね。
まず、ステップ1は、QR法を適用する前にAに施す前処理です。
実は、元々のAが、成分に0がないぎゅうぎゅう詰めな行列(密行列)だと、QR法が(ウィルキンソンの移動法込みでも)中々収束してくれません。
実際に筆者が

というエルミート密行列で上記のプログラムを実行したところ、相似変換に267回もかかり、さらに非エルミートな密行列

に至っては、自分のPCのスペックではファンが激しく回るだけで計算が全然進みませんでした。
それを防ぐために、予め成分に0の多い疎行列にAを相似変換してからQR法に持ち込みます。
変換先の疎行列は、Aがエルミート行列なら「三重対角行列」、Aが非エルミート行列なら「ヘッセンベルグ行列」となります。前者への変換方法が「ランチョス法」、後者への変換方法が「ハウスホルダー変換」となります。
この前処理に関しては次回、次々回で説明します。
ステップ2,3については、QR法では固有値が下の行から求まっていくので、固有値が新しく求まるたびに行列のサイズを小さくして、その都度移動量μの値を更新します。行列のサイズを小さくすることで計算量を抑制するわけです。
これまで例題に用いてきた行列

はすでに三重対角行列になっているエルミート行列なので、前処理は不要でそのままQR法に持ち込めるので、「行列のサイズを小さくする(減次)」と「移動量μをその都度計算する」という2つの修正を新たに入れればよく、それを反映させ実装すると次のようになります。


このプログラムを実行すると、
![]()
相似変換の回数がオリジナルのQR法の36回、単純にウィルキンソンの移動法を追加したQR法の22回に対して、たった10回で済みました。およそ計算回数がオリジナル比で1/4に減ってますね。
この計算回数削減効果は、元のAのサイズが大きければ大きいほど絶大なものになります。
次回、次々回は、QR法の前処理に使用される「ランチョス法」、「ハウスホルダー変換」について紹介します。