皆さん、こんにちは。
今回は、4で割って1余る素数は必ず2つの平方数の和で書けるという「フェルマーの2平方和定理」と、関連して「ガウス素数」の話題も簡単に紹介します。
0. フェルマーの2平方和定理とは?
フェルマーの2平方和定理とは、次のような定理です。

2は2=1^2+1^2と書けるので当然成り立っているのですが、4で割って1余りさえすれば、その素数は必ず2つの平方数の和で書けるというのです。ちょっとびっくりしませんか?
具体例として、試しに100以下の「4で割って1余る」素数を全て調べてみると、

このように全てについて、確かに2つの平方数の和で表現することができています。
なぜこんな性質が成り立つのか、証明していきたいと思います。
以後、4で割って1余る素数を「4m+1型の素数」と呼称することにします。
1. 平方剰余の相互法則
さて、フェルマーの2平方和定理を証明するための準備として、補題として次の定理「平方剰余の相互法則」を証明します。

素数pが4m+1型なら、pで割って余りが-1(つまりp-1)となる平方数が必ず存在するという定理であり、「平方剰余」とは、平方数を素数で割った時に余りになりうる整数の事を表します。
(大学入試でしばしば「平方数を3,4で割った余りは0か1」という知識を使いますが、この0,1が平方剰余の例です)
「平方剰余の相互法則」は実はもっと広い定理なのですが、今回のメインテーマであるフェルマーの2平方和定理を証明するのに必要十分な特別な場合に絞って紹介しています。
証明の方針ですが、pで割って余りが-1になるような平方数を一つでも見つければいいので、実際にそのような平方数を構成してきます。
4m+1型の素数pをそのまま
![]()
と定義して、天下り式ではありますが、ここから(p-1)!を考えます。
実際に(p-1)!を計算すると、

という4m個の積にかけます。
ここで、両脇から1つずつ数字を拾って1セットの積にすると、次のようになります。

ここで、mod pの合同式を考えてあげれば、

(p-1)!がとある平方数と合同だと示すことができました。
(p-1)!という数を見てピンと来た人もいるかもしれません。ウィルソンの定理ですね。
a^p, (p-1)!を素数pで割った余りは? ~フェルマーの小定理・ウィルソンの定理~ - ちょぴん先生の数学部屋 (hatenablog.com)
ここで、ウィルソンの定理から、

(p-1)!が-1と合同だと言えるので、この2つを合体させれば、

となり、これで証明は終わったも同然ですね。
題意を満たす自然数xとして、例えば

を採用すれば、その平方数はpで割って-1余ることになります。
これで、pで割って-1余る平方数を見つけることができたので、平方剰余の相互法則の証明が完了です。
注意すべきは、pで割って-1余る平方数が⑤の形だけとは限らないことです。⑤の形が題意を満たすことは証明しましたが、それ以外の平方数が題意を満たさないことは一切証明していません。
まぁ、いずれにせよ、pで割って-1余る平方数が最低でも1つあることは保証されています。
2. フェルマーの2平方和定理の証明
さて、これで準備が完了したので、本題であるフェルマーの2平方和定理の証明に移っていきます。

2-1. p=2の場合
最初に、明らかに例外扱いとなっているp=2の場合について見てしまいます。
p=2の場合は前述の通り、
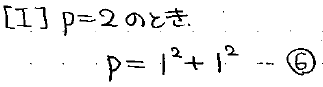
とかけるので、定理の成立は明らかです。
よって、以降はpが4m+1型の素数の場合に絞って考察します。
2-2. p=4m+1の場合における、(←)の証明
まず、左方向、つまり「pが2つの平方数の和で書ける⇒pは4m+1型」を証明します。
こちらは、平方数を4で割った余りが0か1になるという大学入試でもお馴染みの知識を使えば簡単に示せます。

この結果の対偶を取れば、4m+3型の素数はどうあがいても2つの平方数の和で書けないことが分かります。
問題は、右方向、つまり「pが4m+1型⇒pは2つの平方数の和で書ける」の証明です。この証明がかなり難しいわけです。
2-2. p=4m+1の場合における、(→)の証明
いきなりですが、次のような条件(T)を考えます。

自然数kをある値に固定したときに、それと4m+1型素数pの積kpが平方数の和で書けるか否か?それを問うています。
もしそれができるなら「その自然数kは条件(T)を満たす」と表現し、できないなら「その自然数kは条件(T)を満たさない」と表現することにします。
2-3-1. 条件(T)を満たす自然数kは最低でも1つは存在することの証明
ここで、先ほど証明した「平方剰余の相互法則」から、

を満たす自然数aが最低でも1つは存在します。そして⑧をよく見ると、これは条件(T)でy=1としたものになっています。a^2 + 1がmod pで0ということは、a^2 + 1はpの倍数ということになるので。
つまり、自然数kをうまく選んであげれば、条件(T)の式⑦は(x,y)=(a,1)という整数解をもつことが分かります。
このことから、条件(T)を満たす自然数kは最低でも1つは存在することが分かります。
ここで、今後の議論のためにaの値に制限を加えておきます。具体的には、aがp/2未満という制限を付けます。
もし、aがp/2以上

だとすると、
(※mod pで考える場合にはpで数字が一巡するので、aはp未満で考えれば十分です)
![]()
という新たな自然数bを考えると、bはp/2未満で

となり、aだけでなくbも平方剰余の相互法則を満たす自然数xの1つとなっていることが分かります。
つまり、p/2以上の自然数が平方剰余の相互法則を満たす自然数xの1つなら、対応するp/2未満の自然数もまた平方剰余の相互法則を満たす自然数xの1つになります。
よって、aはp/2未満と考えてしまっても一般性を失いません。

このとき、(x,y)=(a,1)が⑦の解になるようにkを選んであげると、次のように不等式評価できます。

よって、条件(T)を満たすp/2未満の自然数kが最低でも1つは存在することが分かります。
こうして、p/2未満の小さな自然数kに対しても条件(T)を満たす可能性が出てきたわけですが、ではそんなkの最小値が何なのかが気になってきます。
次では、条件(T)を満たす自然数kの最小値が実は1になるということを、無限降下法というテクニックを使って証明したいと思います。
2-3-2. 条件(T)を満たす自然数kの最小値が1であることの証明(by 無限降下法)
条件(T)を満たす自然数kの最小値をk0とし、背理法によってk0=1となることを証明します。
背理法を使うので、誤りを証明したい仮定を準備します。今回の場合は、
![]()
k0が2以上という仮定をおきます。
この仮定の下、k=k0において、⑦が(x,y)=(x1, y1)という0以上の整数解を持つとします。

このとき、x1とy1は0以上の整数A,Bと、整数x2, y2を使って

と書くことができます。
但し、x1, y1をk0で割った余りx2, y2は、絶対値が最小になるようにとります。つまり、次のような制限を付けます。

文字だとイメージが付きにくいですが、例えば「3で割った余りが2ならより絶対値が小さい-1と余りを読み替える」のと一緒の事をしています。
さて、⑯を⑮に代入してmod k0を取ると、

が成り立つことが分かります。よって、左辺はk0の倍数なので、0以上の整数nを使って
![]()
と書けることになります。この時点ではx2=y2=0となる可能性があるのでnが自然数とは限らないことに注意です。
なのですが、実はn=0は不適です。
もしn=0だとすると、

のようにpが表現でき、さらに先ほど示した⑬により

が言えるので、
(※条件(T)を満たす自然数kがp/2未満の範囲に最低でも1つあることを言ってるのが⑬で、今はそんなkの最小値k0を探っているので、当然ながらk0はp/2未満です)

となってしまいます。
こうなると、⑳からpは2以上の2つの自然数の積になってしまい、pが素数であることと矛盾してしまいます。
よって、めでたくnは自然数でなければいけない、とわかります。
このとき、⑲に戻って不等式評価すると、⑰によって、

と自然数nが評価できます。
さて、話が長くなってきたので、今回やりたい証明の結論を前もって説明しておきます。
それは、「k0≧2を仮定すると、k0未満の自然数kについても条件(T)を満たしてしまう」です。
この結論は当然ながら「条件(T)を満たす自然数kの最小値がk0」という設定と反してしまい矛盾となるわけです。
このように「『ある条件を満たす最小の自然数』を設定すると、特定の操作によって、その条件を満たす『もっと小さい自然数』が作れちゃう」ことを示すことで矛盾を導く方法が、無限降下法です。
この無限降下法というテクニックは、以前に紹介した「フェルマーの最終定理のn=3,4の場合の証明」でも使用している、整数問題ではよく登場する証明テクニックです。
フェルマーが余白に書き残した証明 ~フェルマーの最終定理のn=4の場合の証明~ - ちょぴん先生の数学部屋 (hatenablog.com)
フェルマーの最終定理のn=3の場合の証明 - ちょぴん先生の数学部屋 (hatenablog.com)
この無限降下法を念頭においたうえで、先に進みます。
矛盾を導くために、「2つの平方数の和」を新しく拵えます。
⑮と⑲を掛け算すると、

のように、左辺が2つの平方数の和の形で書けます。1,2行目の左辺を展開すると確かに同じ式になります。
全体をk0^2で割ってあげると、

となり、もし、

が両方整数なら、㉔の左辺は2つの平方数の和になりますね。
x3, y3の分子についてmod k0を取ると、
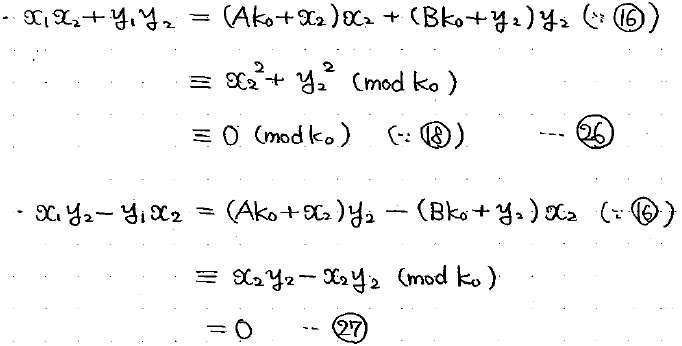
なんと両方とも0、つまり分子は両方ともk0の倍数ということになります。
k0の倍数をk0で割ったものがx3, y3なのですから、x3, y3は両方とも整数になります。
この事実と、これまで示してきた不等式を積み重ねると、
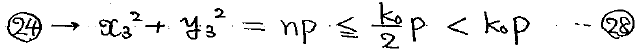
k0未満の自然数nが条件(T)を満たしてしまうことが分かります。
これは「条件(T)を満たす自然数kの最小値がk0」という設定と明らかに矛盾します。
これでようやく、k0≧2という仮定から矛盾が導けました。
よって、背理法により、最小値k0があるとすれば
![]()
となるしかありません。
そして、平方剰余の相互法則によりk0の存在は保証されているので、条件(T)を満たす自然数kの最小値k0は1だと確定します。
以上から、

つまり、pが4m+1型素数なら、pが2つの平方数の和で書けることが証明できました。
これにて、フェルマーの2平方和定理の証明は完了です。
このフェルマーの2平方和定理に関連して、「ガウス整数」「ガウス素数」の話題を取り上げます。
ガウス整数とは、実部と虚部の両方が整数となる複素数の事で、いわば通常の整数を拡張した概念です。
ガウス整数の中でも、絶対値が1になるものを「単数」と呼びます。単数は±1と±iの4つのみが存在します。

単数は、「素因数分解」をガウス整数の範囲にまで拡張したときに、通常の素因数分解における「1」に相当する複素数です。
そして、次の性質を持つガウス整数を「ガウス素数」と呼びます。

例えば、4m+3型の素数は必ずガウス素数になります。3を例にすると、
![]()
という4パターンに素因数分解されますが、いずれも単数×自身(の派生形)の形になっています。
しかし、素数ではあってもガウス素数ではないものがあります。それが、2と4m+1型の素数です。
これらの素数は、フェルマーの2平方和定理から2つの平方数の和で書けるので、共役な2つのガウス整数の積に因数分解できてしまいます。例えばこんな感じに。

よく、数学のジョークとして「2や5は実は素数じゃないんだ」というネタが取り上げられますが、それはこのように複素数の範囲にまで拡張すると2と5が因数分解できてしまうからです。
でも、2や5はあくまで「ガウス素数ではない」だけであって、通常の実数の範囲では間違いなく素数です。そこは誤解しないようにして下さい。