高校で「2次方程式」を勉強すると、どんな2次方程式であっても解ける魔法の公式を習うはずです。
もう何度も呪文のように唱えて暗記したはずの公式ですね。この解の公式の心は、各項の係数だけを使って、方程式の解を計算できることです。
2次方程式を習った後には「3次方程式」を勉強します。そこでは、
「因数定理」を使って因数分解を繰り返して
(1次式)×(1次式)×(1次式) =0 ないし、(1次式) × (2次式)= 0 の形にして解くんだ!! と習います。
実際、高校の教科書や大学入試で出題される3次方程式はほぼ100%この解法で解くことができ、できない場合は必ず誘導が付きます。入試問題を解いていてこの形にできない場合は、十中八九計算ミスを疑うべきです。
とはいえ、「3次方程式にだって、2次方程式みたいな万能な解の公式があるはずだ」と考えるのは至極当然のことですね。
実際、3次方程式の解の公式はあり、今日では「カルダノの公式」と呼ばれています。
だったら、「最初からそれを教えろや!」と思いたくなりますが、この記事を最後まで読むとわかるのですが、最終結果が非常に汚く、手軽な手計算でどうにかなる代物ではありません。高校の教科書に載らないのにも理由があるわけです。
まさにタイトル通り、
「人は、カルダノの公式を使うことでどんな3次方程式も解き明かす。しかしそれは、解く人の寿命をも縮める、まさに最後の手段なのだ!」 (元ネタはわかる人にはわかるはず笑)
なんです。あくまで、どうしても因数定理でうまくいかないときの最後の手段、アルテマウェポン程度に考えておいてください。
では、今回は、そんなカルダノの公式を導出してみます。
0.まずは結論から・・
3次方程式の解の公式、カルダノの公式は下のようになります。
3次方程式 ax^3 +bx^2 +cx +d =0 (a≠0)の解は、



と文字を置くと、

となります。(ω: 1の3乗根のうち虚数のもの)
[訂正] pの式の1項目1/3Aは不要です。無視してください。また、pの式の2項目の係数は正しくは-1/3です。
どうですか?3段階に渡って文字の変換をしたのでスッキリしたように見えますが、元のa~dの式に直すと、とんでもなく複雑な式になってしまうことがお分かりいただけるかと思います。2次方程式の解の公式の時点で蕁麻疹が出る人がこれを見たら失神どころではすまないでしょうね。
これが、冒頭で実用性が皆無といった所以になります。なので、3次方程式はできる限りこの公式を使わなくて済むように因数分解を考えて解くのが普通です。
とはいえ、どうやってこんなヘンチクリンな式ができるのかが気になると思うので、導出していきます。
1. (step1)立法完成→2次の項を消す
スタートは、以下の3次方程式です。

ただしa=0だと2次方程式以下になってしまうので、a≠0で考えます。
まずは、文字が4つあるところを3つに絞りたいので、①全体をaで割り算すると、
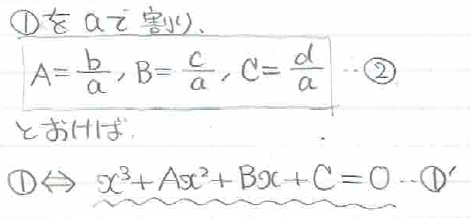
3次の係数を1にできます。これで文字を3つにすることができました。これをさらに簡単にするために、xを変数変換します。
天下り式ではありますが、以下のようにxをyに変換します。

騙されたと思って、この③を代入してみると、次のようになります。

[訂正] 1次の係数の1項目1/3Aは不要です。無視してください。また、1次の係数の2項目の係数は正しくは-1/3です。
こんな変換をして何が嬉しいか?係数こそ複雑ですが、「2次の項」が消えています!
2次方程式を解くとき、2次+定数=0の形に変形し、この作業は「平方完成」と呼ばれるのでした。この平方完成の要点は、「1次の項」を消して式を簡単にすることです。
これと同じように、3次方程式の「2次の項」を消去する作業を「立法完成」と言います。
係数を文字で置き換えると3次方程式は以下のように少しスッキリします。

[訂正] pの式の1項目1/3Aは不要です。無視してください。また、pの式の2項目の係数は正しくは-1/3です。
↓

この形にできても、方程式を解くのはまだまだ難しいので、次の行程でさらにテクニカルなことをします。
2. (Step2)急がば回れ→あえて2文字に分ける
2次の項が消えた方程式①'''を解くために、あえてこんなことをします。

せっかくyという1文字だった未知数を2文字に分けてしまうのです。一見すると解決から遠のいたように見えるのですが、これが解決への糸口になります。この急がば回れな発想が、カルダノの公式の凄いところです。
とりあえず、①'''に⑤を代入すると、次のようになります。
 ・・①""
・・①""
この式を満たす(s,t)の組み合わせを探していくのですが、ここは、次のような関係を満たす(s,t)に絞って探していくことになります。

この⑥⑦が成り立てば①""が成り立つことはすぐに分かりますが、①""が成り立つからと言って⑥⑦が成り立つとは限らないことに注意が必要です。つまり、⑥⑦は、①""が成り立つ「十分条件」であって、「必要条件」ではありません。
しかし、⑥⑦を満たす(s,t)の組み合わせが仮に3つ見つかれば、それが①""を満たす解のすべてだということができます。なぜなら、3次方程式の解は全部で3つしかないからです。よって、⑥⑦を満たす(s,t)が3つ見つかればいいなぁと願いつつ、探し始めましょう。
3. (step3) 2次方程式の解と係数の関係を使って、(s^3,t^3)を探す
⑦を3乗すると、


となります。すると、⑥と合わせてs^3とt^3の和と積の値が分かります。この形を見れば、高校数学でお馴染みの「2次方程式の解と係数の関係」が浮かびます。つまり、s^3とt^3は、次の2次方程式の解になっています。

この2次方程式を、解の公式を使って解くと次のようになります。

s^3とt^3は対称なので、求まった解の片方をs^3, もう片方をt^3と好きに割り振って構いません。とりあえず、ここまでで、(s^3, t^3)の組み合わせが求まりました。
このとき、√の中身が「2乗+3乗」の形なので負になることがある、つまりs^3とt^3が虚数になる場合があることに注意しましょう。
4. (step4) 3乗根をとる。
ここまでで言い忘れていたことがあります。step3の最初でしれっと⑦を3乗していました。


しかし、よく考えると⑦→⑦'は成り立っても、その逆⑦'→⑦は複素数の世界では必ずしも成り立ちません。具体例を挙げてみましょう。
例えば「x^3 = 1ならば、x=1」は正しいでしょうか?実数の範囲では正しいです。しかし、複素数の範囲まで広げると正しくありません。複素数の範囲まで広げると、x^3=1となるxは1以外に、x=(-1±√3i)/2のもう2つがあるのでした。
ここまでの注意で何が言いたいかと言えば、⑦'だけ考えてしまうと、⑨を満たすs,tは各々3種類、計(s,t)の組み合わせが9通り存在してしまいます。この9通りの中から、⑦を満たす組み合わせを抽出しないといけないということです。
つまり、
 を満たすからと言って、
を満たすからと言って、
 を満たすとは限らない。という点に注意せよ、ということです。
を満たすとは限らない。という点に注意せよ、ということです。
これから、少しややこしい話をします。
今、⑦を満たす(s,t)の組み合わせの一つを、

と「表記する」ことにします。但し、

です。なぜ「表記する」と強調したかというと、複素数の累乗根の性質に由来します。
(※訂正:ルートの中のpは3乗です)
分かりやすい例を挙げると、虚数単位iを習ったとき、
「x^2 = -1 を満たすxの一つを、iと表記する」のでした。2乗したら-1になる複素数は2つあって、そのうちの1つを「iと書くことにしましょう」というルールなのです。片方をiと書けば、もう一方が-iと書けることになります。虚数は、文字通り実態を持たない数なので、どっちにiと名前を付けても問題がないわけです。
話を戻せば、9通りある3乗根(s,t)の組み合わせのうち、⑦を満たしてくれる都合のいい組み合わせの1つに

と名前を付けます。という話です。複素数の累乗根にはこういったややこしさがあるので注意です。
さて、⑦を満たす(s,t)の組み合わせは⑪だけでしょうか?実はあと2つ見つけることができます。具体的には、次のようになります。

(ωは、1の3乗根のうち虚数のもの)
⑪の片方にωを、もう片方にω^2をかけたものになります。ω^3=1という性質を使えば、これらの(s,t)が⑦を満たすことは簡単に分かります。
s,tはそもそも

で定義されたのですから、これによってyが無事3つ求まりました。

yの3次方程式

の解が3つ見つかったので、全て探し切ったことになります。
5. (step5) xの式に戻す
あとは、変数変換を一通り巻き戻すだけです。結果、

が導出されました。(Q.E.D)
いかがでしたでしょうか?これが3次方程式の解の公式、カルダノの公式です。
前述のように、実際に方程式を解くための式にしては複雑すぎるので実用性は皆無です。しかし、歴史的意義としてはとても大きいです。
この公式が発明されたのは16世紀になってからです(2次方程式の解の公式は、紀元前の古代ギリシャでは既に知られていました)。当時は「虚数の存在」が信じられていない時代でした。しかし、a~dが全て実数であったとしても、3次方程式を解く過程で必然的に虚数ωが登場するので、この公式によって、多くの数学者が虚数の存在を認めざるを得なくなったわけです。
その後、4次方程式の解の公式通称「フェラーリの公式」が発明され、5次以降の方程式の解の公式が存在しないことが証明されました(四則演算と有理数乗の組み合わせで全ての解を表現しきれないという意味です)。その証明の過程で「群論」という数学の一分野が生まれ、数学のみならず物理学にも応用され大いに発展することになります。
2020年の年内の投稿はこれで最後になります。コロナ禍で大変な1年になりましたが、来年もよろしくお願いいたします。
それでは、皆さまよいお年を。
<導出全貌>
[訂正] pの式の1項目1/3Aは不要です。無視してください。

