皆さん、こんにちは。
![]()
今回は、数学の世界で最も美しい数式と言われている「オイラーの等式」について紹介します。
1. オイラーの公式の証明

を証明します。ご覧頂いて分かる通り、「虚数」を使うことで「指数関数」と「三角関数」が繋がるという画期的な公式です。
[Step1: e^x, sinx, cosxのテイラー展開]
テイラー展開については、以前「バーゼル問題の証明」の記事で取り上げたことがありますが、初見の方のためにもう一度説明します。
参考:バーゼル問題の証明
「テイラー展開」とは、関数を多項式の和の形で書くことです。式にすると①式のようになります。
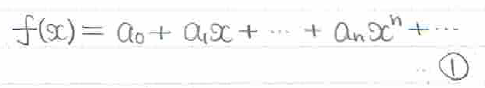
anの一般項は、①式をn回微分してx=0を代入することで求まります。
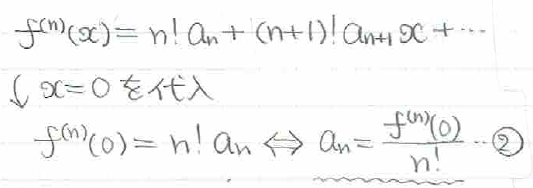
①②をまとめると、一般に関数f(x)のテイラー展開は③のようになるわけです。

さて、ここでe^x, sinx, cosxという3つの関数についてテイラー展開を実行してみましょう。
最初に、指数関数f(x)=e^xは、何度微分しても形が変わらないのでテイラー展開は④’式のようになります。

各係数が階乗の逆数になっているのが特徴です。
次に、三角関数f(x)=sinx は、微分するとcosx → -sinx → -cosx → sinx ・・・と4個周期で回るので、テイラー展開は⑤’式のようになります。

奇数次の項だけが生き残って、係数はe^xと同じく階乗の逆数で符号が互い違いになっています。
同様にf(x)=cosxのテイラー展開は⑥’式のようになります。

sinxとは逆に偶数次の項だけが生き残って、係数はe^xと同じく階乗の逆数で符号が互い違いになっています。
こうして3つのテイラー展開の式を並べてみると、よく似た形になっていることが良く分かります。



[Step2: e^xのテイラー展開にx=iθを代入]
ここで、④’式にx=iθを代入して、iの付いている部分(=虚部)と付いていない部分(=実部)に分けてあげると、

⑤’式、⑥’式から、見事に実部がcosθ, 虚部がsinθとなって、オイラーの公式が証明できました!
2. オイラーの等式
(1) 導出
こうして証明された「オイラーの公式」

に、θ=πを代入すると・・・

となります。
この結論の式、
![]()
こそが、数学の世界で最も美しい数式と称される「オイラーの等式」です。
(2) なぜ美しいのか?
改めて鑑賞してみましょう。
![]()
まず、とってもシンプルですよね。
しかも、ネイピア数e, 円周率π, 虚数単位iという、数学の世界で最も重要な数たちが一堂に会しているわけです。
ここで、この3つの数の由来を振り返ってみましょう。
1. ネイピア数e
この数は、以前の記事で書いたように金融の分野から生まれ、この数を公比にして出来る指数関数e^xは何回微分しても形が変わらないという稀有な性質を持っているのでした。
極限、微積分を取り扱う「解析学」という分野で登場する数です。
2. 円周率π
この数は、小学校でも習う「円周と直径の比」を表す数で、図形を取り扱う分野「幾何学」から生まれた数です。
3. 虚数単位i
この数は、2次方程式を解くために「2乗するとマイナスになる数」として発明された代物で、方程式などを取り扱う分野「代数学」から生まれた数です。
このように
「解析学」「幾何学」「代数学」という数学の3分野からそれぞれ、全く独立した経緯で誕生した3つの重要な数が、たった一本の数式で繋がっている。
これがオイラーの等式の美しさの所以であり、神秘なのです。