皆さん、こんにちは。
今回の記事では、以前ご紹介したバーゼル問題

を証明しようと思います。
↓バーゼル問題の紹介記事
様々な証明の仕方がありますが、1本目の今回は、第1発見者のオイラーが見つけた証明方法をご紹介します。これが最も分かりやすい証明だと思います。
<証明の概略>
オイラーの発見した証明方法は、大まかには以下のような流れになります。
sinxを2通り(1. テイラー展開, 2.無限積表示)で表す→3.係数比較
ということで、上記の3ステップで証明していきます。
[Step1: sinxのテイラー展開]
「テイラー展開」とは、関数を多項式の和の形で書くことです。式にすると①式のようになります。
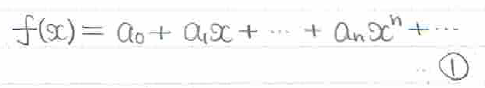
anの一般項は、①式をn回微分してx=0を代入することで求まります。
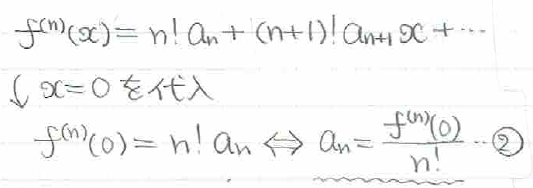
①②をまとめると、一般に関数f(x)のテイラー展開は③のようになるわけです。

さて、今回の証明ではsinxをテイラー展開したいので、f(x)=sinxを代入します。
sinxは微分を繰り返していくと、cosx→ -sinx→ -cosx→ sinx→・・と4周期でループするので、x=0を代入した値は④式のようになります。

ここで、n≡1(mod4)は、nを4で割った余りが1、という意味です。
④式の結果を反映させれば、sinxのテイラー展開は下のようになります。

奇数次の項だけが生き残って、プラスとマイナスが交互になる、そんなテイラー展開になっています。
これでStep1は終了です。
[Step2: sinxの無限積表示]
Step1ではsinxを足し算の形で表現していきましたが、今度はsinxを掛け算の形で表現していきます。
ここで、y=sinxのグラフを思い出すと、sinxは「xが円周率πの整数倍の時」0になるのでした。数式化すると⑤式のようになります。
 ・・・⑤
・・・⑤
このとき因数定理を使うと、sinxは以下のように因数分解できそうです。

x-(πの整数倍)を全て掛け算した格好です。しかし、このままでは不都合です。
この因数分解の式を展開してみてください。例えば1次の係数が
π×2π×3π×・・・・・となって無限大に飛んで行ってしまいます。これはStep1で証明したsinxのテイラー展開の式

と明らかに矛盾します。
ということで、因数定理の本質を損ねず、かつテイラー展開の式と矛盾しないように、因数分解の書き方を工夫してみましょう。
その極意は、1次の係数が「1」となるようにすればよいのですから、下のようにしてはどうでしょうか?

この(B)式のように因数分解すれば、x=0,π, 2π・・を代入すれば0になるという因数定理の本質を失わず、かつ先頭のx以外の定数項だけ全てかければ1なので、1次の係数は1になります。
この(B)式が、sinxの無限積表示となり、Step2も終了です。
[Step3: (A)(B)の係数比較]
これで役者は揃ったので、バーゼル問題を証明していきます。
(A): sinxのテイラー展開、(B): sinxの無限積表示、を再掲します。


両者は、同じsinxという関数を2通りで表現したものなので、(B)を展開したときの係数は(A)の係数と当然一致しているはずです。
ということで、(B)を展開します。
(B)式の上下のカッコは「和と差の積」になっているので、先に計算してしまうと下のようになります。

先頭のx以外のカッコの部分を一気に展開します。定数項と2次の項以外はどうでもよいので、この2つのみに着目すると(B)'式のようになります。
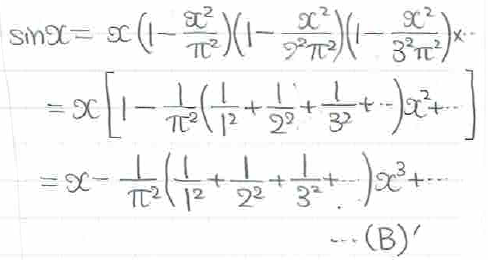
これで、直接(A)(B)式が係数比較できる形になりましたので、3次の係数を比較してあげると、、、

となって、見事バーゼル問題が証明されました!!
最初にsinxを使おうと思いついたオイラーは流石の天才だと思いますね。。。
このようにしてオイラーは「ただの分数の足し算なのに、最終的に円周率πが登場する」という奇妙で美しい真理に辿り着いたわけです。