このシリーズでは、山梨大学医学部後期の数学の問題を解いていきます。
7回目の今回は2016年です。
第1問(1)
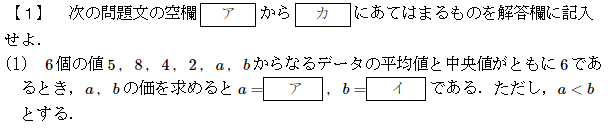
データに関する問題です。
まず平均値の情報からa+b=17が求まり、あとはa,bの大小関係で場合分けして中央値が6になるようにしていきます。
ポイントは、5と8の間(間に中央値の6がある)にaとbがどう入るかで場合分けすることです。
<筆者の解答>


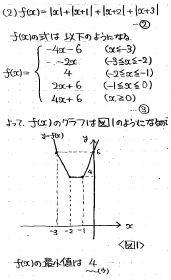
第1問(2)
![]()
絶対値付きの関数の増減についての問題です。
xの値による場合分けで絶対値を外してグラフを描けば十分です。
<筆者の解答>
第1問(3)

球面に内接する正四面体に関する問題です。
エについては、OA=OBが半径になるので瞬殺ですね。
オについては、AB=2√2となるので、C(a,b,c)がTの頂点になるとするとAC=BC=2√2となり、かつOC=OAとなります。
<筆者の解答>

第1問(4)

関数の増減を調べる問題です。
Sn=Σpk, Tn=Σqkとして、xの累乗と1-xの累乗をまとめてあげると見通しが良くなります。あとは微分して終了です。
<筆者の解答>

第2問(1)
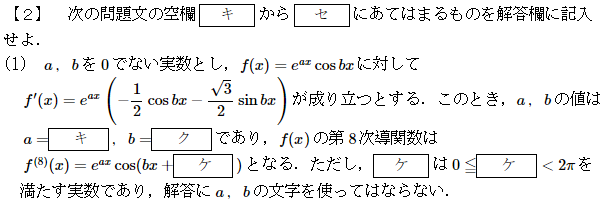
指数関数×三角関数の微分に関する問題です。2019年にも似たような問題が出題されていましたね。
8回微分を計算するのは中々にしんどいので、前と同じように「ライプニッツの公式」を利用するというのが高校範囲での解法になります。
ただ、この解法だと二項係数の場合分けと計算が必要で、最後の三角関数の合成の部分でミスりそうですね。
ここは、大学数学の範囲にはなりますが「オイラーの公式」を使うことで簡単に解くことができます。f(x)が微分しにくい要因が指数関数と三角関数が混在していることなので、オイラーの公式を使って三角関数を指数関数に置き換えて「f(x)を微分しやすい指数関数だけにする」というのが心です。
つくづく複素数は偉大ですね。
<筆者の解答>

※オイラーの公式を使う別解です。

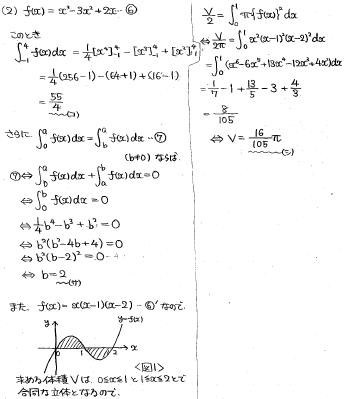
第2問(2)

積分計算と回転体の体積を計算をする問題です。
コについては教科書レベルの積分なので、計算ミスにだけは注意しましょう。
サについては、左辺と右辺を独立して計算してては日が暮れてしまうので、右辺を移項することでaを消去してしまうとよいでしょう。具体的にはf(x)の0~bの積分=0となります。
シについては、y=f(x)の0≦x≦1での形状と1≦x≦2での形状が合同なことに気付けると計算量を節約できます。
<筆者の解答>
第2問(3)

複素数の計算と、特定の複素数を解に持つ整数係数のn次方程式を求める問題です。
問題文の条件は、z^7=1と言い換えられます。これを使うとスにおけるz^(n^2)の指数の肩を小さくすることができます。
その状態で2乗を計算すると、問題文の条件が直で出現してzがすべて消えてくれます。
セは、スの結果を直接利用すればよいです。w=2+z+z^2+z^4とするとスをwの2次方程式に置き換えることができ、その2次方程式はそれ以上整数係数の1次式で因数分解できないので、これが答えになります。
<筆者の解答>
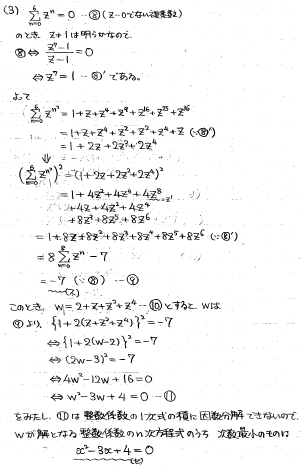
第3問

確率の問題です。趣旨としては、不利なAに対してどんなハンデを与えれば公平になるかを調べる問題ですね。
Aが優勝する条件は、Aがn-1勝しBがk勝した状態で、Aが最後に1勝することです。但しkは0以上4以下の整数です。
よって、Aが優勝する確率pnの式を調べて、nに直接n=1,2,3,4を代入して値を調べていく形になります(pnはΣを含んだ式になり、綺麗に解き切ることができません)。
<筆者の解答>

第4問

3つの自然数について最大公約数、最小公倍数を考える問題です。
d=(a,b,c)とおいて、a,b,cがどんな式で書けている必要があるかをひたすらに調べていきます。どの数とどの数が「互いに素」なのかを注意深く追いながら左辺を計算して右辺になることを確かめていく必要があります。
最小公倍数ですが、a=Ad, b=Bd (d=(a,b) )とすると、[a,b]=ABdと書くことができます。
<筆者の解答>

第5問

楕円の交点に関する問題です。
CαとCβの式を連立することで、交点(x0, y0)が求まります。その一方で、(x0, y0)でのCαとCβの接線の傾きが調べられるので、その積が-1になることを確かめていきます。
<筆者の解答>

第6問
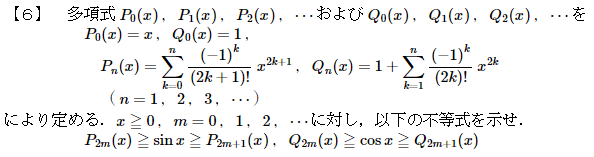
不等式証明の問題です。この問題の背景にはsinxとcosxの「テイラー展開」があります。
試しにPn(x)とQn(x)を一回微分すると、Pn'(x)=Qn(x), Qn'(x)=-Pn-1(x)となることが分かります。この事実が後の証明に大いに役立ちます(この式自体がsin, cosっぽさを醸し出してますね)
この問題は、mについての「数学的帰納法」で証明していくと見通しが良いです。
つまり、まずm=0について証明し、次にm=kでの成立を仮定してm=k+1で成立することを証明する、という段取りです。
その各々について、各辺の差を取って微分して単調増加性を利用する、という典型的な手法を使えばよいでしょう。
今回証明した2つの方程式でm→∞としてあげると、はさみうちの定理によりPn(x)はsinxにQn(x)はcosxに収束することが分かります。つまり、sinx=P∞(x), cosx=Q∞(x)となり、Pn(x)とQn(x)は正しくsinxとcosxのテイラー展開になっているというわけです。
<筆者の解答>

