リーマン予想シリーズのパート4です。
前回の記事で、調和級数

は無限大に飛ぶことを説明しました。では、似たような無限級数、

は収束するのでしょうか?それともオルガ級数なのでしょうか?
この級数は、ちゃんと収束してくれます。
証明は次のようになります。
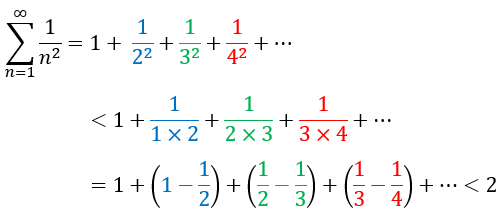
ここでもトリッキーなテクニックを使います。
級数の各数字の分母が整数の2乗になっているので、その1つを1小さい数に置き換えています(2行目)。すると分母が小さくなるので、全体としては大きくなります。
次にこの分数一つ一つを引き算の形に書き換えます(3行目)。すると1/2,1/3といった数字たちが次々と消えていくので、最終的にこの級数は「2より少し小さい数」より小さい数といえるわけです。
2より小さいことはわかりましたが、具体的にどんな数に収束するのかはまだわかりません。400年前の昔、とある数学者が

は最終的にいくつになるか? という問題を出しました。
この問題、当時としてはかなりの難問で、90年もの間誰にも解けませんでした。
ところが、かの天才数学者オイラーが、ついに解き明かすことに成功します。
これに因み、スイスのバーゼルがオイラーの故郷だったことからこの問題は「バーゼル問題」と呼ばれるようになりました。
オイラーが導き出した、驚愕の答えがこちらになります。

みなさん、これの何が凄いかわかります?
もともと私たちは只の分数の足し算をやっているはずでした。ところが、その果てにあったのは、分数の足し算とは一見全く関係のなさそうな「円周率」だったのです!!
「只の分数の足し算の答えが円周率になる。」
数学の世界に潜む神秘そのものだと思いませんか?
ちなみにexcelで書かせると下のようになります。

π^2/6は、1.6449くらいの値になるのですが、途中からその値にピタッと張り付いている様子が分かるかと思います。
このバーゼル問題の解き方は、色々あります。
先日取り上げた 今年の慶応医学部の第3問は、まさにこのバーゼル問題を高校数学の範囲で解く問題だったわけです。
(2020年慶応医学部 第3問)

大学数学の飛び道具を使えば、もっと簡単に証明することができ、「テイラー展開」「フーリエ級数展開」などを使うことになります。これらは、このブログで機会があれば紹介したいと思います。
その後、オイラーは同様の方法で、

なども証明していき、もっと一般化して、

のように○○乗の部分を文字sに変えたものを研究し始めました。これはsの関数となり、「ゼータ関数」といいます。
(s=1としたのが調和級数、s=2としたのがバーゼル問題 ということになります)
このゼータ関数こそが、このシリーズの大目標だったリーマン予想の主役になります。
だからこそ、これまで調和級数や、バーゼル問題の話をしてきたというわけです。
ただ、ここまでの話で「素数」の話題は出てきませんでした。
ということで、次回は、このゼータ関数と素数がどういう関係にあるのかを紹介していきたいと思います。
ではでは。