リーマン予想シリーズ その5です。
前回紹介した、ゼータ関数

がリーマン予想の主役になると言いました。
一方で、最初の記事でリーマン予想は素数に関する問題だ と言いました。
しかし、ここまでの議論では、ゼータ関数が素数と何の関係があるんだ?ってなってしまいます。今回は、ゼータ関数と素数のつながりについて紹介していきます。
(※数学的に厳密な議論を端折った、大雑把な議論となっていますが、雰囲気だけでも掴んでいただければと)
さて、ゼータ関数の式をいじくってみましょう。
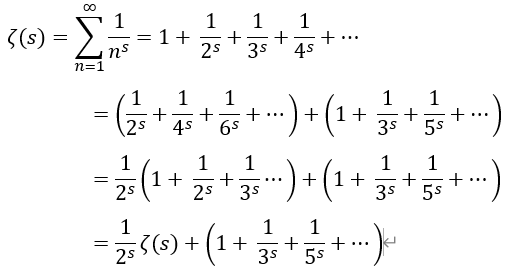
まず、分母が偶数となるものを抜き出してみます。すると、当然それらは2で括ることができ2で括ってあげると、ゼータ関数の形がそのまま出てきます。よって、ζで整理してあげれば、

となります。これで、右辺には分母が奇数のものだけが残りました。次に、この奇数たちから3の倍数となるものを抜き出し、同じように変形してみます。

すると、分母が奇数だけの足し算が出てくるので、そこを置きなおしてζで整理すると、

となって、右辺には分母が3で割り切れない奇数だけが残ります。
同じようなことを、5の倍数、7の倍数、11の倍数と素数の倍数に着目してやっていけば、最終的には右辺には1だけが残ります。

よって、ζにかかっている係数で割り算すれば、

とゼータ関数を表現することができました。
ここでΠはΣと同じように掛け算を表す記号で、この式の意味するところは、
「ゼータ関数は、すべての素数を使った掛け算で表せる」ということです。
s=1の場合は、調和級数で無限大に飛ぶのですから、当然、

となります。これは、以前紹介した「素数は無数に存在する」の別証明となっています。もし、素数の個数が限られていれば、掛け算が無限大になるはずがないですから。
s=2の場合は、バーゼル問題なので、

となります。
この式は、「素数をすべて使えば円周率を表現できる」ことを意味しています。
今まで不規則な数字の羅列と考えられていた素数から円周率を作ることができたということで、素数には何かしら法則性があるのでは?と考えられるようになりました。
そして、このようにゼータ関数は「すべての素数の情報を持っている」関数なので、
このゼータ関数を掘り下げていけば、いずれ素数の性質が明らかになるだろうということになります。
リーマン予想とは、まさに「ゼータ関数って、こんな性質を持ってるんじゃね?」という一大予想なわけです。それが証明できれば、素数の核心に大きく迫ることができるという意味で非常に大事な問題なわけです。
というわけで、いよいよ次回は、リーマン予想の言わんとしているところを、大雑把にではありますが、紹介していこうと思います。
ではでは