皆さん、こんにちは。
本日は、大分頭が混乱する話をしようと思います。
すばり、
1+2+3+4+・・・の結果が、なんと-1/12になる!
という話です。
「んなわけないやろ!どう考えたって無限大に発散するやろ!何で収束してしかもマイナスになるんや!?」
というツッコミはごもっとも。しかし、この結果はあながち間違いとは言えないのです。どうして「あながち間違いとは言えない」という歯切れの悪い言い方になっているかも含めて、解説していきます。
1. 実数の世界での解析接続 ~グラフをどう拡張するか~
今回のテーマを理解するには、「解析接続」という概念を知っておく必要があるので、先にこれについて解説します。
簡単に言うと、「範囲の限られたグラフを、滑らかに延長すること」です。
「滑らかに」の意味は、連続(=途切れていない)かつ微分可能(=接線の傾きが変化しない)になるように、と言う事です。
具体例を挙げて説明します。
今、-5≦x≦5で定義された放物線y=x^2があったとします(図1)。

図1
x≧5 (要するに定義域の外側)の部分にグラフを滑らかに延長したいと考えたとき、どう延長すればよいでしょうか?
一番安直な延長の仕方は、x≧5でも引き続きy=x^2のグラフを描くことです(図2)

図2
しかし、連続かつ微分可能な(=滑らかな)延長の仕方は、この1通りではありません。
例えば、x≧5で、y=50 - (x-10)^2 のグラフを描いてあげると図3のようになります。

図3
他にもx≧5で、y=10x - 25 のグラフを描いたものは図4のようになります。

この3つの延長の仕方は、「x=5で連続で微分可能」なので、どれも滑らかな延長の仕方になっています。
x=5で連続かつ微分可能でありさえすれば、どんな関数を繋げても「滑らかな延長」となります。
2. 複素数の世界での解析接続
先ほどは、連続かつ微分可能でありさえすれば、どんな関数を繋いでも「滑らかな延長」になると説明しました。
しかし、その話が成り立つのは実は「実数の世界」でだけなのです。複素数の世界にまで話を広げると事情が変わってくるのです。
複素数を変数にして複素数を返す関数、「複素関数」についても、
「滑らかな延長」=「繋げるポイントで連続かつ微分可能」
という定義自体は変わりありません。
しかし、複素関数で事情が変わってしまうのは、ひとえに「複素関数の連続・微分可能という条件が、実数関数のそれに対して比べ物にならないほど厳しい」からなんです。
今、改めて微分の定義を載せると、f'(a)は下のようになるのでした。

何気なくlimの所に「h→0」と書いてありますが、0への近づけ方は色々あります。
それら全ての近づけ方について、上の極限が同じ値になって初めてf'(a)が計算できる=微分可能なわけです。
実数関数の世界では、変数が1文字だけなので近づけ方は1次元的に「左から近づく」「右から近づく」の2通りしかありません。なので、「微分可能になる」条件は、この2方向の極限が等しくなるだけで良いので、かなり緩いわけです。

しかし、複素関数の場合、変数はz=x+iyで、実部xと虚部yの2種類があるので、近づけ方が2次元的になります。よって、360°あらゆる方向から近づくことができるわけです。

複素関数の場合、これらありとあらゆる方向から近づいた時、どの近づき方でも極限値が一致しないと、「微分可能」にならないわけです。
このように、複素関数での「微分可能」というのは非常に厳しい条件なのです。
(※それゆえに、微分可能な複素関数には「正則関数」という特別な名前までついています)
3. 一致の定理
話を「解析接続」に戻しましょう。
解析接続とは、「連続かつ微分可能になるように、滑らかに関数を延長する」ことでした。
実数関数の場合は、微分可能という条件が簡単に実現できるので上述のように延長の仕方がいくらでもあるのでした。
しかし、複素関数の場合は「微分可能」という条件をクリアするのが非常に難しいので、延長の仕方が大分限られてきそうです。
サブタイにある「一致の定理」というのは、実は「この延長の仕方が1通りしかない」という定理です(証明はここではしません)。
先に上げたy=x^2の例では、複素関数と解釈した場合には延長の仕方が「y=x^2を継ぎ足す」しかない、ということです。

この一致の定理は、次のように言い換えることもできます。
「2つの複素関数f(z)とg(z)があって、f(z)とg(z)はある一部の形状が完全に一致するとする。このとき、f(z)とg(z)は全領域に渡って全く同じ形状であると言える。」
「一部が同じなら全部が同じである」何気に物凄いことを言っています。
この一致の定理を使うことで、タイトルにある、
1+2+3+・・・= -1/12が示せてしまうのです!!
4. 無限等比級数の公式における解析接続
ここから、1+2+3+・・・= -1/12の証明に入っていきます。
そのための道具として、無限等比級数の公式で解析接続を行います。「解析接続」「一致の定理」は、この例で理解するのが一番簡単だと思います。
初項1, 公比xの等比数列の無限和は、よく知られているように①式のようになります。
 ・・・①
・・・①
まずは①式の左辺に注目してみましょう。
よく考えてみると、等比数列の和が発散せずに収束ためには公比xが-1<x<1を満たしていないといけません。これ以外のxの値では収束せず意味のある値になりません。
言い換えれば、①式の左辺は「定義域が-1<x<1」ということになります。
一方、①式の右辺に注目すると、分母に1-xがあるので、x=1以外では問題なく値を計算することができます。
言い換えれば、①式の右辺は「定義域がx≠1」ということになります。

この時、左辺の定義域を「無理やり右辺の定義域に広げる」としたら、どうしたら良さそうでしょうか?
ここで「一致の定理」を使うわけです。
2つの定義域の共通部分は-1<x<1で、この中では左辺も右辺も全く同じ値を取るわけです。つまり、-1<x<1での形状が完全に一致するわけです。一致の定理によれば「一部が一致していれば、全部が一致する」のでした。
だから、本来-1<x<1でしか意味のある値にならない、

は、-1<x<1の外側では、(無理やり考えるのだとすれば)

と同じ関数だと考えてしまってよい、ということです。
よって、例えば本来定義域から外れているx=-1を①式に代入すると、こんな結果が得られます。

誤解しないで頂きたいのは、これは「1-1+1-1+・・・を計算すると1/2になる」という意味ではない、ということです。
通常の意味では1-1+1-1+・・・は、0と1をひたすら往復する意味のない足し算です。
そんな意味のない足し算に「無理やり意味のある答えを与えるとすれば、1/2が一番妥当な値である」くらいの意味に捉えてください。
5. 1+2+3+・・・=-1/12の証明
準備が終わったので、いよいよ1+2+3+・・・= -1/12の証明をしていきます。
先に登場した①式の両辺を微分すると、②式になります。
 ・・・②
・・・②
この②式についても、①式と同じように、左辺の定義域が-1<x<1、右辺の定義域がx≠1なので、解析接続をすることで左辺の定義域をx≠1に拡張することができます。
②式にx=-1を代入すると、③式のようになります。
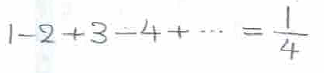 ・・・③
・・・③
この③式を使って、1+2+3+・・・=-1/12を示します。
T=1+2+3+・・・と文字で置いて、ここから③式を無理矢理作ってあげることにより、

という感じに導出できました!!
この結果に関しても、
本来無限大に発散して計算できない1+2+3+・・・に、無理やり意味のある答えを与えるとすれば、-1/12が一番妥当な値だ、という解釈に留めておきましょう。
冒頭で「この結果はあながち間違いとは言えない」という歯切れの悪い言い方をしたのは、これが理由です。
テストで1+2+3+・・・=-1/12と無理やり計算を進めると当然のように×を食らいますので、ご注意ください。
6. 解析接続の使い道
一見すると、このような無理筋な理論に思える解析接続ですが、実はいくつか応用例があります。
最も顕著な応用例は、素粒子物理学で使われる「繰り込み理論」です。
原子核はプラスの電荷をもった陽子と、電荷を持たない中性子から出来上がっていますが、プラスの電荷同士は本来反発するので普通に考えれば原子核はバラバラになってしまうはずです。一か所にまとめようとすると、本来は無限大のエネルギーが必要になるはずなのです。しかし、現実には原子核という塊としてちゃんと存在できています。
この矛盾を解消するために、無限に発散するエネルギーに、解析接続を使って求まる有限値を無理矢理当てはめる、といったことが行われるわけです。(詳しくは専門家でないので説明できません。誤りなどあれば是非ご指摘ください)
他にも、同じく量子力学に登場する「カシミール効果」を説明するのにも、解析接続の知見が不可欠のようです。ここでは、解析接続を使って無理やり当てはめた数字で計算すると、見事実験結果と一致するようです。
一見メチャクチャに見えますが、バカにならないことが分かります。
ここまで物理での応用例を見ましたが、実は数学そのものの問題でも利用されています。その著名な例が、実は以前紹介した「リーマン予想」です。

の値がゼロになるようなsの実部は、必ず1/2だろう、という予想でした。
しかし実はこのゼータ関数、「sの実部>1」の範囲でしか収束しません。実部が1/2というのは、明らかにこの収束条件に反しています。
リーマン予想では、解析接続を使って「s=1以外の全ての複素数sについて値を計算できる」ように、ゼータ関数をイジっているのです。
素数の謎を解明する大きな手掛かりになるリーマン予想にも、根本の部分で解析接続が実は使われていたのでした。
という感じに、今回は摩訶不思議な「解析接続」の世界について紹介しました。