2024年も大学入試のシーズンがやってきました。
今回は、京都府立医科大学の数学に挑戦します。
<概略> (カッコ内は解くのにかかった時間)
1. 合成関数を含んだ方程式(65分)
2. 確率計算と評価(45分)
3. 円に内接する五角形の面積(95分)
4. 回転体の体積(50分)
計255分
<体感難易度>
1<4<2<3
昨年よりも難化したというか、どの問題も重厚で1問あたり平均1時間もかかってしまうぐらいの相変わらず難しすぎるセットです。
第1問はfでゲシュタルト崩壊しそうな合成関数の方程式の問題で、このセットの中ではまだマシな部類ですが、それでも完答しきるのは骨が折れます。これでまだマシって・・・
第2問は確率の問題で、(2)まではスムーズにいくものの(3)の評価が発想力勝負で難しいです。
第3問の五角形の面積は、本セットどころか今年度解いた入試問題の中で一番大変だったかもしれない問題です。とにかく計算が長く煩雑の一言。
第4問の回転体の体積は、ボリュームこそそれなりにありますが何とか押し切れるレベル感ではあります。
<個別解説>
第1問

合成関数を含んだ方程式の問題です。
以後fを何回も書くのが面倒なので、xにn回fをかましてできる関数をfn(x)と呼称することにします。
(1)とにもかくにも、f2(x), f3(x), f4(x)を順に代入して求めていくことに尽きます。
f4(x)=xとなることから、fn(x)は4周期で同じ形になることが分かります。この事実が(2)以降の突破口になります。
(2) Eの左辺をF(x)としてα、f1(α), f2(α), f3(α)を代入すると、どれもfn(x)の周期性から同じ式になり結果はcとなります。
(3)解と係数の関係を利用します。y1+y2の方は(2)の検討からcになるので、示す方程式の1次の係数が-cになることはすぐに分かります。
一方のy1y2については、fn(α)の具体的な式を代入すると綺麗に約分されて-4になってくれます。
(4) (3)の方程式を実際に解いて、そこからαを求めていきます。
<筆者の解答>



第2問

確率計算と評価の問題です。
(1)n-1回目までは表だけが出続け、最後のn回目に少なくとも1枚裏が出ればよいわけです。
(2)Snをp1~pnの和だとすると、そもそもpnがf(n)-f(n+1)の形をとっているので、和を取ると間の項が次々に相殺されていきます。これで無限級数が求められます。
一枚でも裏がでれば終了するこのゲームの都合上、いつかは必ず裏がでて終わるわけなので、pnの無限和が1になるのは当然ですね。
(3)この大問の肝となる評価の問題です。これが難しいです。
p2k-1としてしまうと、(2)のような相殺が起こらず和が計算できません。
そして、p2k-1は等比数列のように見せかけて、指数部分はkの「2次式」です。指数が2次式になってるシグマなんて見たことがありませんよね。
ということで、何とかして不等式評価するしかありませんので、試行錯誤します。
まず、下限の0.6について。こちらは比較的簡単で、p1+p3の時点で0.6を超えてくれます。pnは全て正の値なので、これでPが0.6より大きいことは確定です。
問題は上限の0.62の方です。普通の指数関数よりも指数が2次式な分強く減少していくのでPが収束することははっきりしています。でもその上限値はよく見えてきません。
シグマ計算の障害になっているのが「指数が2次式」なことでしたね。だったら、この2次式をより小さい1次式(底が1/2なので指数が小さければ全体は大きくなる)で評価できないか、と考えが及びます。指数が1次式であれば等比数列なのでシグマ計算が可能です。
p1+p3の時点で0.6よりちょっとだけ大きいという良い精度で評価できていたのですから、p5以降の指数を1次式に取り換えれば上から評価できそうです。
そんな1次式を拵えるにはどうしたらいいか?元の2次式が下凸なことを踏まえれば「接線」を考えればよくないですかね?
この考え方でPを上から抑えると、見事0.62以下の値で評価できます(等比級数の計算自体、途中どんどん大雑把に評価していってます)。
これにて一件落着です。
(3)の不等式評価は発想力のいるかなり難しい問題でしたね。私自身(2)までは10分もかからず解け、ほとんどの解答時間を(3)のアイデア出しに費やしていましたので。
<筆者の解答>


第3問

円に内接する五角形の面積の問題で、個人的には本年度の入試問題最凶の問題ではないかと考えております。
(1)(2)
設定が抽象的なので、まずは初等幾何でどうにかA3Bが求まらないかと考えましたが方法が思いつきませんでした。
初等幾何でうまくいかない以上、もう計算でゴリ押すしかないと決意し、Bがx軸上に来るようにxy座標を設定することにしました。
この方針で進める場合は(2)から求めた方が得策です。
三平方の定理や正三角形の性質、円周上にある条件などを駆使し、A2とA4の座標が求まるまで計算を続けます。この過程で(2)の結果が得られます。
このA2とA4の円周上における中点がA3なので、座標を(cosθ, sinθ)として加法定理を駆使してこの座標をaだけの式で書けるまで計算を続けます。
そうまでしてやっとこさA3Bの長さを求めると、なんと円の半径と同じ1になりました。aに依存せずしかも半径と同じ値、あまりに意味深な値です。
こんな結果だったので、私が思いつけてないだけで、うまく初等幾何を使えばA3Bが半径と同じと示せるのかもしれないですね。後日じっくり考えてみることにします。
(2)五角形は、二等辺三角形A2A3A4と、台形A1A2A4A5の2つに分割できるので、それぞれの面積をこれまでの知識を総動員して計算していきます。
実はここでも∠A2OA3=60°という意味深な結果が出てくるので、やはり初等幾何的な背景が見え隠れします。
おそらく初等幾何でうまく思いつけばこの問題は瞬殺に近いものになるんでしょうが、思いつけなければ上記のような遠大な計算を強いられる、とんでもない問題ですね。
ますます初等幾何での解法を探してみたくなってきました。
[3/5追記]
本問の初等幾何を用いた別解が見つかりましたので追加しておきます。
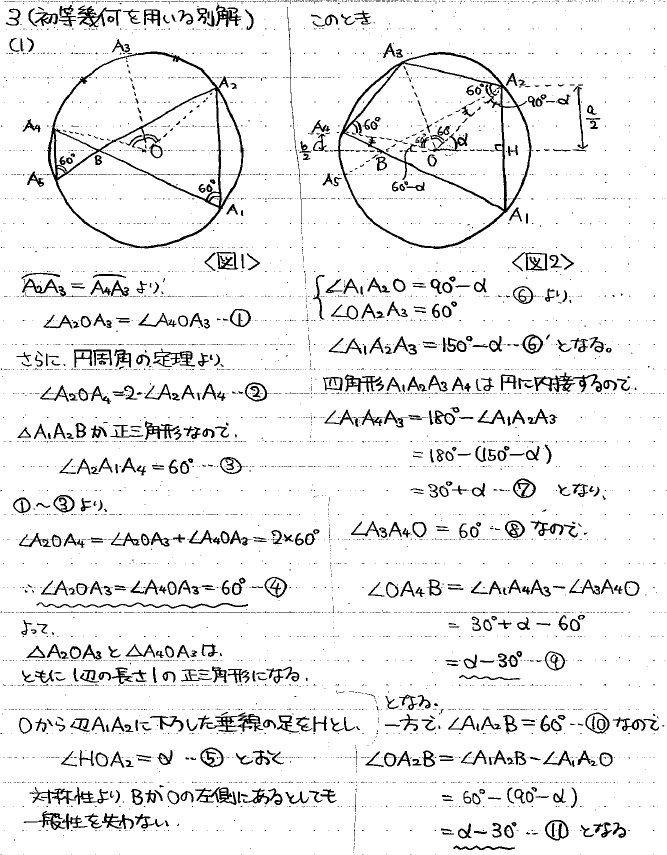
(1)は円周角の定理を用いて正三角形をいくつか作り、円に内接する四角形の性質やその他角度の関係を用いることで、円周角の定理でA2, A4,B,Oが全て同一円周上にあることが示せます。その円は中心A3, 半径1の円になるので、これによりA3B=1が言えます。
(2)(3)三角比をうまく使うことで素早くbの式が求まり、Sの式もスムーズに求まります。
最初に行った座標平面での計算ごり押しで出てきた意味深な結果があったからこそ初等幾何での発想を何とか思いつくことができました。。。
<筆者の解答>




↓初等幾何を用いた別解

第4問

回転体の体積の問題です。
(1)~(3)
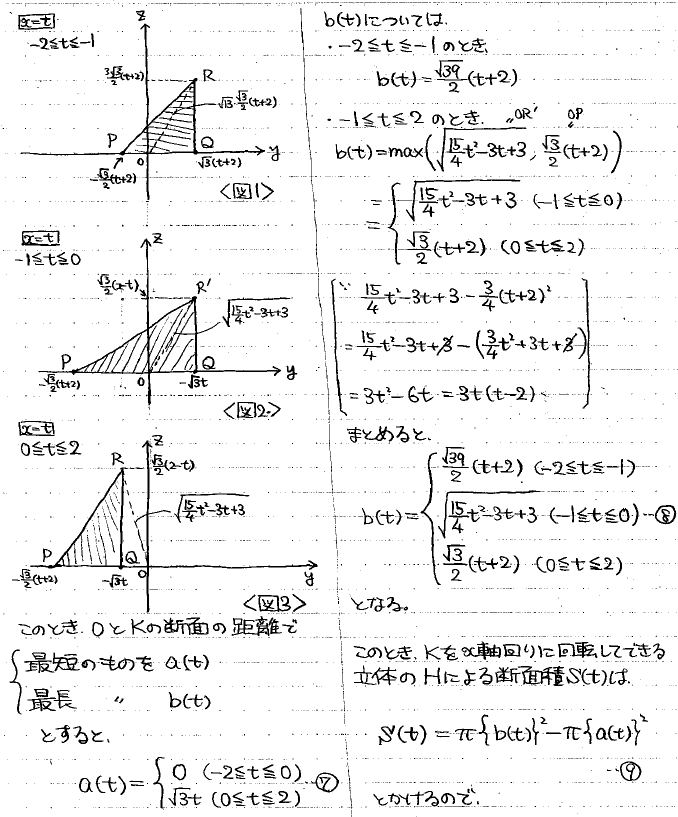
各辺上の点をベクトルでパラメータ表示し、x座標がtになるものを見つける、という作業を6辺分繰り返します。その際、各交点が存在しうるtの範囲を合わせて調べておくと(4)の見通しが良くなります。
(4)ここまでの結果を踏まえ、平面x=tによるKの断面をtの値で場合分けして図示していきます。そして、その断面と回転軸との距離で最短の物をa(t), 最長の物をb(t)としてこれら二つを調べて、その上で断面を回転すると断面は内径a(t), 外径b(t)のドーナツ型になります。
あとはこの断面積を積分すればお目当ての体積になります。
<筆者の解答>