2024年も大学入試のシーズンがやってきました。
今回は、東京医科歯科大学の数学に挑戦します。
今年の秋に東工大と合併し「東京科学大学」となるため、「東京医科歯科大学」としては最後の入試になります。
<概略> (カッコ内は解くのにかかった時間)
1. 整数問題 (35分)
2. 空間ベクトル(50分)
3. 定積分の計算(15分)
計100分
<体感難易度>
3<1<2
「医科歯科大」としての最後の試験となった今回のセットは、こちらも統合先の東工大と同様、奇天烈な問題は影を潜め穏やかなセットだった印象です。
第1問は過去に似たような類題が散見される整数問題です。不等式評価などをその場で考えて組み立てないといけなくて、本番ではやや難な気がします。
第2問は「勾配」なる新規要素を含む空間ベクトルの問題です。が、あまり「勾配」絡みで悩むことはないでしょう。それ以外の要素がむしろ地味に難しかったりします。
第3問は誘導付きの定積分の計算で、誘導がとても丁寧なので完答したいところです。
<個別解説>
第1問

和と積が等しくなる自然数の組み合わせを考察する整数問題です。
(1)a1~anは対称な関係にあるので、問題文のような断りがなくてもa1≦a2≦・・≦anという大小関係は自分で設定すべきです。(2)以降もこの大小関係を前提に考察していきます。
この大小関係を左辺の和の方で適用すればa1a2≦3が言えるのでa1,a2がだいぶ絞れます。
和の方で大小関係を適用する理由は、右辺が積の形になってて約分しやすくなるからです。そして、不等号の向きは、できるだけa1~anの候補が絞りやすい方向に設定するのがコツです。
(2) (1)と同じロジックで評価を行うと、a1×a2×・・・×an-1 ≦nが言えます。
このときに、a1≧2(すべてが2以上)と仮定したときに矛盾が生じることを導く背理法の使用を考えましょう。
(3)a1=a2としたときにa3(≧2)以降がどうなるかを考察します。
すると、(2)までで考えた不等式から2^(n-3)≦a3×・・・×an-1 ≦nがいえるので、この時点でnの候補が絞れます。
絞られたnの候補それぞれについて、対応するa3・・・が存在するかどうかをチェックすることになります。
あと、(2)ではn=2が除外されていたので、この場合を忘れずにチェックしておきましょう。
<筆者の解答>


第2問

空間ベクトルの問題です。
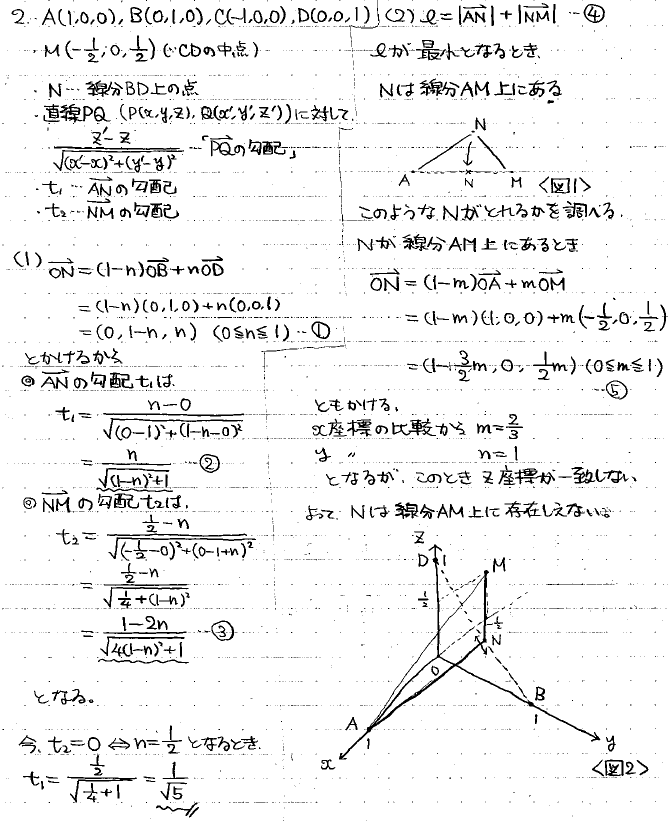
(1)Nの座標をパラメータ表示して、定義通りにt1とt2を計算すればよいでしょう。
(2)今年のセットの中で一番難しく感じた小問です。
lは折れ線の長さになっています。AとMは固定でNだけが動くので、A,N,Mが全て一直線上にある状況が、lが最短になる理想形です。
ところが、Nはどれだけ動かしても直線AM上には乗っかってこないのです。全てが一直線になってくれる夢は敢え無く潰えてしまいました。
折れ線のままで長さを最小化する方法と言えば、「M(orA)と対称な点を作って、その点とA(orM)を結んだ直線とNの軌跡が交わったところがlが最短になる!」が思い浮かびます。
これは座標「平面」では非常に有効な方法でしたが、3次元空間においては「対称っつったって、何とどう対称なんだ?」となってしまうわけです。しかも仮に「対称な点」があったとしても直線と軌跡が交わってくれる保障なんかないのです。よって、この方法も使えません。
ということで、少なくとも最初から図形的な解釈でlを最小化するのは無理そうなので、仕方なくlを式で表現して代数的にごり押します。
lの式は、√(2次式)+√(2次式)の形になっていて、仮に微分したところで大小関係が上手く判定できません。これでまた行き詰まってしまうわけです。
しかし、lの式を、「座標平面内の」折れ線の長さと解釈したらどうでしょう?さっきの「対称な点を作って・・・」という解法が今度こそ使えませんかね?√の中身を平方完成することで、疑似的に座標平面上の点を作り出すことができるので、この方法が使えるようになります。
これでようやくlを最小化できました。
[追記] 読者さんのコメントでとても簡便な別解を教えて頂いたので、紹介します。
それはずばり「展開図」を考えること。
△ADBと△MDBを、同一平面上に展開してしまえば、その時のAMとDBの交点をNとしてしまえばlは最小になるわけです。
(3)単純に0≦t2≦t1をNのパラメータで解けばよいです。
あれ?(2)だけ浮いてない?実は「勾配」の知見を全く使わずに解いたので、ひょっとしたら勾配を使ったらもっと楽に解けるかもしれないですね。
<筆者の解答>

※最後の最後でミスをしていたので、修正しました。
↓(2)の別解です。

第3問

定積分の計算問題です。
(1)これはいわゆる「King Property」を使うタイプの積分です。
左辺と右辺を見比べるとsinxとcosxの違いしかありません。ということで、sinをcosに変換すればうまくいくんじゃないかと思うわけで、t=π/2 -xと置換してみましょう。
(2) 右辺のfの中身にある1-t^2の形をヒントにしたいですね。
左辺にはsinx+cosxという余計なものがあったのに右辺ではきれいさっぱり消えていることもヒントです。
積分変数をxからtに置換するとsinx+cosxを道連れにしてくれる・・・となると、t=sinx-cosxと置換すればいいんじゃないか?と思うわけです。
幸いそう設定するとsin2x=1-t^2になってくれるので、目標達成となります。
三角関数の問題でよく「t=sinx+cosxとおいたときsinxcosxをtの式で表せ」なんてものがあったりしますけど、それの応用を行ったわけです。
この(2)の積分にIと名前を付けておきます。
(3) 被積分関数は、(sin2xの関数)×sinxの形になっているので(1)が利用できて、そうするとsinxをcosxに取り換えた積分も全く同じ値になります。
さらに(2)で調べたIは、この両者を足したものになっています。
よって、今回求めたい積分値Jは、(2)の右辺の形に簡略化できるわけです。さらに言えばf(1-t^2)はtの偶関数で積分区間が符号違いになっているので、積分区間を0≦t≦1と変えたものに変換することができます。
そうすると、1-t^2が√の中に入った関数を積分することになるので、t=sinθと置換するとルートが外れて見通しが良くなります。そうすると分母が上手く2倍角の公式が使える形にできて積分が進むことになります。
<筆者の解答>
