今年度から始まったセンター試験改め共通テストの問題を見ていきます。
次に数学ⅡBを扱います。
※試験当日に解いており、ミスがあるかもしれません。
<略解>

[1/18追記] 採点の結果、全問正解でした。
<個別解説>
第1問[1]
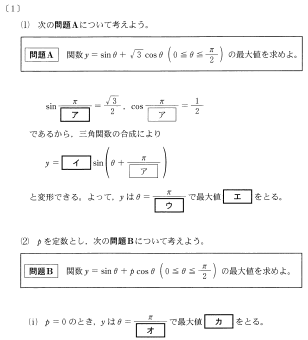

三角関数の最大値を考える問題です。
(1)三角関数の合成です。sinが√3/2, cosが1/2になる角度は60°ですね。それをラジアンに直せばπ/3です。180°=πラジアンと覚えておけばOKです。
yのsinの中身はπ/2を通過するので、そうなる瞬間が最大です。
(2)
(ⅰ)p=0なら、y=sinθなので非常に簡単です。
(ⅱ)三角関数の合成の公式をそのままなぞればOKです。p>0のときはyのcosの中身が0を通過するので、その瞬間に最大値となります。
(ⅲ)p<0のときは、αが鈍角となるので、θ-αが常に負でかつ-πより大きくなります。この範囲では、cos(θ-α)はθが大きくなればなるほど増加していきます。
<筆者の回答>

第1問[2]


大学で勉強する「双曲線関数」を背景にした問題です。
(1) チまでは問題文の通りに計算するのみです。ツ、テにしても2^x = Xと変換してXの2次方程式を解けばよいです。X>0に注意しましょう。
(2) 問題文の通りに計算してみましょう。すると、f(x)は偶関数、g(x)は奇関数になっていて、どことなくf(x)はcosに、g(x)はsinに似ている気がしてきます。
(3)では、(2)で気づいた三角関数とのアナロジーを実証する問題です。センター試験は素早く回答する必要があるので、無駄な計算はせずに済ませたいです。
f(x)はcosの親戚、g(x)はsinの親戚という考えから、三角関数の加法定理の類推から(A), (C)は真っ先に候補から外れるので計算不要です。
(cosは同じもの同士の積の足し算、sinは違うもの同士の積の足し算だったことを思い出すとよいでしょう)
候補は(B), (D)に絞られたので、あとは順に検算しましょう。今回の場合は運よく(B)が正しいとすぐに仕留められます。
今回登場したf(x), g(x)のような関数(厳密には底がネイピア数eになったもの)を、双曲線関数と呼びます。
f(x), g(x)がcos, sinとそっくりな性質を持っていることは偶然ではないことが、大学に入ると分かります。キーワードは「オイラーの公式」です。簡単に言ってしまうと、複素数の世界では指数関数と三角関数が密接に繋がっている、ということです。
<筆者の回答>

第2問[1]


2次関数の接線と、それにまつわる面積に関する問題です。
ア:これは一目瞭然でしょう。
イ、ウ:関数を微分してx=0を代入すれば接線の傾きが求まります。それを使って接線の式を求めましょう。
エ:ここまでの考察から、1次の係数と定数項が一致していればx=0での接線が一致することが分かると思います。
オ~コ:ウまでと同じ作業をすればOKです。x軸との交点を求めるのも容易です。
サ~ス:図を描いて積分を計算します。
セ:cをbの式として直せば比例の関係にあることが分かります。
<筆者の回答>

第2問[2]


3次関数の増減についての問題です。
ソ~ト:前問のア~キとやることは全く同じです。
ナ:h(x)を微分して増減表を書けばOKです。xが負の部分で極大値をもちx=0で極小値0を持つことが調べられれば十分でしょう。
ニ~ノ:h(x)=0を解けばOKです。
ハ:h(x)のグラフから、極大値を取るxの値を答えればOKです。
<筆者の回答>

第3問




統計学の問題です。
多くの受験生が、第4問の数列と第5問のベクトルを選択するでしょうから、この第3問の解説需要はあまりないかもしれません。ですが、一応解説します。
(1) 100人中k人が読書をしない確率は、P(X=k) = 100Ck × (0.5)^k ×(1-0.5)^(100-k)で計算できます。確率分布がこのように書けるとき、確率変数Xは、「二項分布B(100, 0.5)に従う」といいます。Xが二項分布B(N, p)に従うとき、平均E(X)はNpで、分散V(X)はNp(1-p)で計算できます。標準偏差は、分散の平方根ですね。
(2)以降は正規分布を使いまくります。サンプルの数が十分に大きい時に、正規分布に近似できることは「中心極限定理」なんて言われたりします。統計学の分野で一番大事な関数が正規分布である理由です。
(2)
(1)で、母比率が0.5の場合はXの平均が50, 標準偏差が5だと計算しています。
もしXが正規分布に従っているなら、Y=(X-50)/5という新しい確率変数Yを考えると、Yは「標準正規分布=平均0, 標準偏差1の正規分布」に従います。正規分布表と言われているのものは、この標準正規分布の数値データになります。
X≦36をYの言葉で言い換えるとY≦-2.8になります。よって、正規分布表のY≦-2.8の部分の面積を計算すれば確率が求まることになります。
母比率が 0.4の場合も同様に二項分布から平均と標準偏差を求めて、同じように確率を計算します。√6の評価が必要になってしまうためか、大小関係のみを訊かれています。
最も、母比率が0.4=平均40人のほうが36に近い数字なので確率が大きそうだというのは、直感的にも分かりますが。。
(3)は信頼区間に関する問題です。95%信頼区間というのは、「値がその範囲に収まる確率が95%」になるような範囲のことです。
この問題でやろうとしているのは、100人に調査したときの平均の結果から、高校全体の平均値を予想することです。「95%の確率で平均値はこの範囲にあるんじゃね?」と予想するわけです。
この問題における204という数字は、100人アンケートでの結果で「標本平均μ」と呼びます。母集団の標準偏差が150だと分かっているとき、100人アンケートでの「標本偏差σ」は、150/ √100 =15で計算されます。
このとき、確率変数Z= (M-204)/15 (確率変数Mは高校全体での平均値)が、標準正規分布に従います。
通常95%信頼区間というと、正規分布の両側から2.5%分の面積を引いて考えることになります。ここまでの知識を総合することで、信頼区間を計算できます。
m, C1, C2の関係性については、信頼区間の意味が「C1≦m≦C2となる確率が95%」だったので、逆を言えば5%の確率で外すこともあるわけです。よって、いつもmがこの区間にいるとは限らないため、スの答えは③です。
(4) 100人アンケートでの平均値はアンケートの度にばらつくので、36より必ず大きい・小さいとは断言できません。
(5) (3)で行った信頼区間の計算の過程でお分かりになるかと思いますが、標本平均μの値によらず、区間の幅は一定になることが分かります(区間の幅は、サンプル数100人と、母標準偏差150だけで決まるため)。よって、正解の一つは④です。
が、(4)の通り標本平均μはアンケートの度にいくらでもばらつくので区間の位置は全く流動的で決まった大小関係は断言できません。よってもう一つの正解は②です。
この正規分布を使った統計学は、ヨビノリさんの解説動画が非常に分かりやすいのでご覧になるとよいと思います。今回の問題に該当する動画を載せておきます。
<筆者の回答>


第4問


数列の問題です。
(1)
ア、イ:等差数列、等比数列の一般項なので、教科書レベルです。
ウ~キ:問題文の指示通りに計算しましょう。等比数列で割り算するというテクニックは、2次試験でも頻出の漸化式の解き方です。
ク:⑤式がnの恒等式なので、nの係数が0でないといけません。そうすると右辺も0にならざるを得ず、pが確定します。
(2)
ケ~ス:それぞれ等差数列、等比数列の和の公式です。
(3)
セ、ソ:⑥式をcn+1について解くだけです。
タ:(1)の結果を代入すれば、cnの係数がただの数字になります。
(4)
チ:これまた⑦式をdn+1について解くだけです。
ツ、テ:u=0はすぐにわかりますし、チ/qが公比ですから、0<チ/q<1を考えればOKです。
余談ですが、(3)(4)における「初項3」って何だったんでしょうね?全く使いませんでしたが。設問自体も尻切れトンボな印象ですし。
<筆者の回答>

第5問




正五角形の対角線、正12面体を題材にしたベクトルの問題です。
基本的に誘導に乗っていけば解くことができる設問になっており、一見空間図形ですが、ほとんど平面図形の範疇で解けるので気負う必要はありません。
アイ: 角を〇ポチで表現して、二等辺三角形の性質を使って埋めてあげましょう。すると、〇15個分で正五角形の内角の和540°になることが分かります。
ウ~オ:長さの比を考えればよく、今回は1辺が長さ1なので考えやすいです。
正五角形の対角線の長さに(1+√5)/2という黄金比が登場するのはあまりに有名な性質です。
カ~ク:a^2を計算すればOKですね。
ケ~サ:長さの計算式を展開すれば内積が登場するので、それを使って解きます。
シ、ス:内積を素直に計算しましょう。計算ミスを極力減らすため、途中まではaを入れたまま計算するとよいと思います。
セ:直感的にほぼ明らかですが、B2DベクトルとOB2ベクトルが等しいという情報で平行四辺形まで確定でき、スの結果から長方形であることまで確定できます。あとは、面の合同性からOB1=OB2も言えるので、正方形で確定です。
<筆者の回答>

