皆さん、こんにちは。
以前、本ブログでは、素数にまつわる未解決問題「リーマン予想」について連作記事を上げていました。
この導入記事の中で、
「通信に使われている暗号システムの根幹に素数が使われている」
と言及しました。
今回は、その暗号システムであるRSA暗号について取り上げていきます。
※RSAとは、この仕組みを発明した3人の科学者の名前の頭文字で、それぞれRonald Linn Rivest氏、Adi Shamir氏、Leonard Max Adleman氏です。
1. RSA暗号の仕組み
1-1.公開鍵暗号
RSA暗号は、「公開鍵暗号」と呼ばれる暗号の1種ですので、まず「公開鍵暗号」の仕組みから解説していきます。
今、Aさん(送信者)が、mという文章をBさん(受信者)に送るという状況を考えます。
Aさんが「送信」ボタンをクリックした瞬間何が起こるかをまとめたのが、下の図になります。
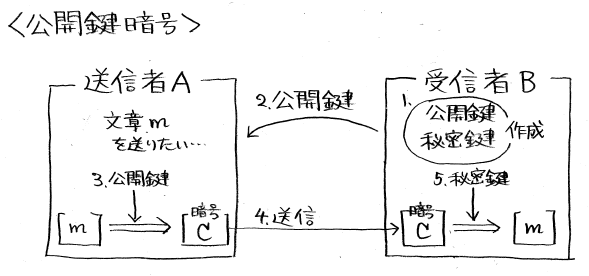
1. Bさんは「公開鍵」「秘密鍵」という2つの鍵を作る
2. Bさんは「公開鍵」だけをAさんに送る
3. Aさんは、Bさんから貰った「公開鍵」を使って、文章mを暗号化する(暗号化された文章をCとする)
4. Aさんは、暗号文CをBさんに送る
5. Bさんは、「秘密鍵」を使って暗号文Cから元の文章mを復元する
外に漏れる鍵は暗号化用の「公開鍵」だけで、復元用の「秘密鍵」は受信するBさんしか持っていないので、暗号文CがBさん以外に解読される心配がない、というのが、この公開鍵暗号の肝です。
1-2.RSA暗号
では、上記の公開鍵暗号の一種であるRSA暗号は、どういう仕組みで「公開鍵」と「秘密鍵」を作って、どうやって暗号化と復元を行っているかを見ていきましょう。
まず、鍵の作り方の概略は以下のようになっています。

このように、巨大な2つの素数p,qを使って公開鍵をn,aの2つ作り、さらにその公開鍵から秘密鍵bを作っています。
次に、暗号化と復元の方法は以下のようになります。

文章を鍵を使って累乗して、それをnで割った余りを考えています。
ここで、文章であるmやCをあたかも数字かのように扱って累乗していますが、デジタルデータの実態は2進法の数字なので、mやCは正しく数字です。
2進法だろうが10進法だろうが割り算の結果には影響がないので(あくまで数字を表現する方法が違うというだけ)、上記の説明で特に破綻は起きません。
1-3.具体例
せっかくなので、具体的な数字で実験してみましょう。
まず2つの素数p,qを用意するんでした。今回は、
p=5, q=7で考えることにします。
(本来はp,qは巨大な素数なのですが、分かりやすさの都合上、小さめの素数を使っています)
すると、1つ目の公開鍵nは、
n=pq=5×7=35となります。
次に、(p-1)(q-1)=4×6=(2^3)×3と素因数分解できるので、
2つ目の公開鍵aは、これと互いに素な自然数、例えばa=5とおけます。
秘密鍵bは、a×b=5×bを(p-1)(q-1)=24で割ったら1になるような1以上24未満の自然数なので、計算するとb=5と求まります。
このとき、m=4として、mを公開鍵n=35,a=5を使って暗号化すると、
C=m^a÷nの余り=4^5÷35の余り=9
となり、これを秘密鍵b=5を使って復元すると、
C^b÷nの余り=9^5÷35の余り=4となって、mと一致します。
2. 暗号文を秘密鍵で復元できる理由
上記の方法で、きちんと暗号文Cから元の文章mが復元できる、というのがRSA暗号の凄い所なのですが、何故このように復元できるのかを、数学的に証明していきます。
2-1. 秘密鍵bが一意に決まることの証明
本題に入る前に、秘密鍵bが、公開鍵n,aから一通りに決まってしまう事の証明を補足でやっておきましょう。
これには、以下のような「余りバラバラ定理」(私の造語です)を証明すれば十分です。

証明の流れは、pで割った余りが一致する2つ以上の数があると仮定して矛盾を導く背理法になります。

この「余りバラバラ定理」から、a,2a,・・・・,(p-1)aをpで割った余りには、1,2,・・・,p-1の全ての数字が1回ずつ登場することが分かります。
ということで、a,2a,・・・・,(p-1)aの中にpで割って1余る数が必ず1個あるということになり、bが1通りに決まる、というわけです。
2-2.フェルマーの小定理
さて、本題に戻ります。復元がうまくいくことの証明には、「フェルマーの小定理」が必要なので、こちらについて説明します。
フェルマーの小定理とは、以下のようなものです。

証明には、先ほど示した「余りバラバラ定理」が活躍します。最後の場面で、pが素数であるという性質を使っています。

このフェルマーの小定理は整数問題を解くにあたって時々登場するもので、大学入試においても証明問題が出題されたことがあります(阪大2010年後期第1問)。こちらは別の証明方法となりますが、一応参考までに。
平成の阪大理系後期数学 -2010年- - ちょぴん先生の数学部屋 (hatenablog.com)
2-3 証明
それでは、復元がうまくいくことの証明を行っていきます。
mとCの定義と暗号化・復元の手順から、結局
「m^abをnで割った余り=m」となることが証明できればOKです。

このように最後の局面で「フェルマーの小定理」を利用するわけです。
3. なぜRSA暗号は安全な暗号なのか?
以上、RSA暗号の概略を見てきましたが、RSA暗号には致命的な弱点があります。
それは、「第3者が公開鍵n,aから秘密鍵bを作成できたら暗号が破られてしまう」ということです。実際、nからpとqを復元できれば、aを使ってbを作ることができるわけです。
しかし、現在のところRSA暗号はそうした脆弱性を突かれることなく安全に運用されています。なぜでしょうか?
3-1. 素因数分解の難しさが、暗号の安全性を担保している
先ほど、暗号を破れる条件として「nからpとqを復元できれば」と言及しました。実は、この「nからのpとqの復元」が非常に困難だから、RSA暗号は安全なのです。
例えばですが、441671、という数字をいきなり見せられたとします。皆さんは、この数を即座に素因数分解できますか?
実は441671=443×997なのですが、この素因数分解はすぐには思いつかないでしょう。
逆に、443×997という計算式を見せられたら、筆算でも何でもして、答えが441671と比較的簡単に求められるはずです。
このように、「掛け算は容易だけど、素因数分解は難しい」というのが一般的なのです。
「そりゃ人間だと難しいだろうけど、コンピュータならすぐに計算できるんじゃないの?」というツッコミがあるでしょう。でも、現状ではコンピュータですら素因数分解はまともにできないというのが実態です。
素因数分解を行う方法というのは今でも原始的なもので、その数を2,3,5,7・・・と小さい順に素数で試しに割ってみる(いわゆる「試し割り」)、しかないのです。
441617=443×997くらいの小さめの数ならコンピュータで瞬殺でしょうが、200桁級の巨大な数の素因数分解となると、コンピュータをもってしても10億年オーダー!!の時間がかかってしまうそうです。これじゃ、生きてるうちに素因数分解を完了するなんてできるわけがないですね。
そういうわけで、第3者が公開鍵nを素因数分解してp,qをゲットするというのは全く非現実的なわけです。p,qの情報がなければ秘密鍵bは作れないので、bを作って使えるのは最初にnを作った(そのためにp,qを最初に準備した)本人だけ、ということです。
このように、通信の安全性は「素数」が担保しているわけです。
3-2. もしリーマン予想が解かれると?
さて、このRSA暗号に関して、よくこんな話が聞かれます。
「もしリーマン予想が解かれて素数の規則性が判明してしまうと、素数を使っているRSA暗号は簡単に破られてしまう!通信の安全性の危機だ!!」
結論から言うと、この煽り文句は「ウソ」です。
リーマン予想が解かれることで分かるのは、あくまで(かなり誇張しても)「素数がどういう規則で並んでいるか」ということだけです。
RSA暗号の安全性を担保していたのは「素因数分解の困難さ」だったので、素数の並び方の法則とは別に、「現実的な計算時間で効率よく素因数分解を行えるアルゴリズム」が開発されない限りRSA暗号は破られません。
とはいえ、リーマン予想の解決が全くRSA暗号の安全性を脅かさないというわけでもないです。素数の規則性は分かってくるので、上記の「試し割り」に使う素数の候補を厳選することができて、計算の手数を多少は緩和できるようになるでしょう。ただ、それが仮にできたにせよ、上記の10億年という天文学的な時間スケールの前では焼け石に水でしょうね。
ということで、皆さん焦ることなく安心してRSA暗号の恩恵にあずかりつつ、リーマン予想という世紀の難問が解かれる日を楽しみに待つことにしましょう。