このシリーズでは、名古屋大学の後期の数学の問題を解いていきます。
10回目の今回は1995年です。
第1問(情報学科)(a)

空間内の直線に関する問題です。
P,Qの座標をパラメータ表示し、l1,l2の各方向ベクトルとPQが垂直になるようにP,Qを決めていきます。
<筆者の解答>
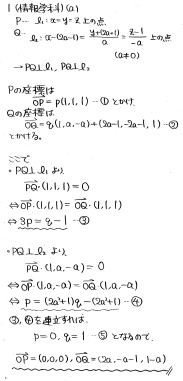
第1問(情報学科)(b)

1次変換の問題ですが、正直行列の成分が本当は違うんじゃないかと感じる悪問です。
(1)xは定数、yは1次関数となるので、基本的にはLpは直線となります。しかし、a=0のときだけ例外です。
(2)関係というのもよく分からないので、とりあえずPとLpを図示しました。
(3)xが実数全体を動くので、Lpの通過領域はxy平面全体、という何とも言えない答えが出て来ます。
<筆者の解答>

第2問(情報学科)(a)

積分方程式の問題です。
定積分の部分を定数でおいて処理する、という典型問題です。
<筆者の解答>

第2問(情報学科)(b)

不等式が成立する条件を調べる問題です。
左辺ー右辺の増減を調べる、という素直な方法だと、a~cが色々入り組んでcだけ取り出せなくなってしまうのでうまくいきません。
ここは、両辺をxで割ってしまえばcが綺麗に分離出来て考えやすくなります。
最後の局面では極限計算が要求されますが、微分係数をうまく使うと計算できるパターンです。
<筆者の解答>

第3問(情報学科)(a)

確率の問題です。
Pn, Qnの導出はともに基本的です。これが求まってしまえば、最終的には3次不等式の処理にできます。
<筆者の解答>

第3問(情報学科)(b)

積分方程式の問題です。
定積分の部分を定数でおいて処理する、という典型問題です。
<筆者の解答>

第1問(工学部)

球面と平面の配置に関する問題です。
(1)Sの中心と半径を調べて、平面と中心との距離dが半径以下になればSとKは交点を持ちます。
(2) 円錐の体積はdを使った方が綺麗に求まるので、それを微分しましょう。
<筆者の解答>

第2問(工学部)

ニュートン法に関する問題です。
問題文のようにxnを決めて√aの近似値を調べる方法をニュートン法と呼びます。
(1)接線の式を調べてあげればよいでしょう。
(2)相加相乗平均を使うと、xn>√aを仮定するとxn+1>√aがわかります。xn+1とxnの大小は(1)の式を直接使えばよいでしょう。
(3) (1)の式の両辺で-√aとしてあげて、右辺から無理やりxn-√aを抽出してあげます。
(4) (3)の不等式を繰り返し使うと、はさみうちに持ち込めます。
<筆者の解答>

第3問(工学部)

内サイクロイドに関する問題です。
(1)弧の長さが等しい事を利用すればよいです。Pの座標は回転行列も駆使すると見通しよく計算できます。
(2)対称性から、0≦t≦120°の部分を3倍すれば面積が求まります。tへ変数変換しつつ積分計算あるのみです。
<筆者の解答>

第4問(工学部)

確率の問題です。
(1)確率漸化式を立てて考えていきます。このとき、BかDにいる状態は対称性からまとめられることに気付けると見通しが良くなります。
(2) YがAにいる確率は、対称性からXがCにいる確率と等しいです。これで(1)の結果が使えると分かります。
(3) 対消滅するまでの2点の配置は2通りしかないので、それを元に確率漸化式を立てるとよいです。
(4) ちょうどn回目で対消滅する確率を求めて、寿命の期待値を計算していきます。最終的には、等差数列×等比数列のタイプのΣ計算が登場します。
<筆者の解答>

