このシリーズでは、大阪大学の後期の数学の問題を解いていきます。
3回目の今回は2010年です。
第1問

多項式の展開から、「フェルマーの小定理」を証明する問題です。
(1) p個並んでいるx1+・・・+xrから、ある因数についてはx1を選び、また別の因数からはx2を選び、と、x1,・・・,xrを1つずつ選んでそれらを掛け合わせることで「多項式の展開」ができるわけです。ということで、求める係数は、「x1を選ぶp1個の因数、x2を選ぶp2個の因数,・・・,xrを選ぶpr個の因数の選び方」と一致します。
(2)展開したときにx1,・・・,xrが2種類以上ある項の係数については、p1~prがすべてp-1以下になるので分母に素因数pが入りません。一方で分子がp!なので素因数pが入っているので、このpが約分されずに残ることになります。
x1^p~xr^pはすべて消えてしまうので、これで係数が全部pの倍数だと言えます。
(3) x1=・・・=xr=1としてあげれば、r^p -r がpで割り切れることになります。rがpで割り切れないので、r^(p-1) -1 がpで割り切れないとダメですね。
この(3)で証明した事実は、「フェルマーの小定理」というもので、整数問題で時々登場するものになります。
※対する「フェルマーの大定理」は、言わずもがな、あの「フェルマーの最終定理」のことです。
<筆者の解答>


第2問

一部を切り取った球の体積を求める問題です。
(1)これはさすがに舐めすぎでしょう笑。半径aの球の体積は4πa^3/3です。
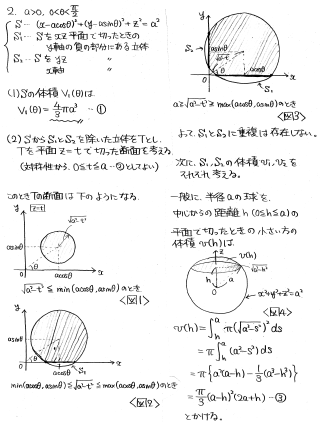
(2)SからS1とS2を削った立体をTとします。定石通りいけば、Tを平面z=tで切った断面積を調べてtで積分する、というのが体積を計算する流れになります。
それでも計算はできるかと思いますが、断面積を計算するのが結構面倒です。ということで、別の方針で体積を計算することにします。
※ただ、断面を描いたこと自体は無駄ではなく、これによってS1とS2に共通部分がないの事が分かるので、S1とS2の体積を独立して計算していいことが分かります。
新たな方針は、先にS1, S2の体積を調べてから、Sの体積からS1,S2の体積を引く、というものです。
S1, S2は、球のうち平面からはみ出した部分という共通点があるので、同じ枠組みで体積を計算できそうです。一般に、半径aの球を、中心からの距離がhの平面で切った時の小さいほうの体積は、積分で容易に計算できます。この知識を使うとよいでしょう。
こうしてS1とS2の体積の合計がaとθの式で求まるので、これが最小になるときV(θ)は最大となります。θで微分して増減を調べましょう。
<筆者の解答>

第3問

回転体の体積を計算する問題です。
(1) f(x)=e^x/(1+e^x)と置いたときに、f'(p)=f'(a)となるpを調べてあげればよいでしょう。
(2)定石通りの積分計算になります。t=e^xと置換してあげれば、部分積分を使って積分計算を進めることができます。
<筆者の解答>

第4問

放物線で囲まれる円に関する問題です。
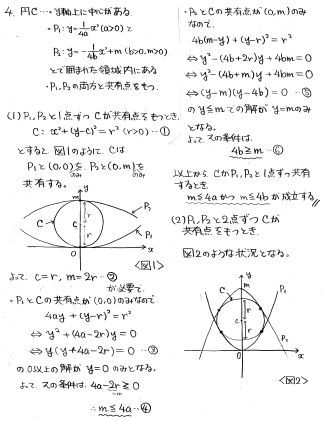
Cの式をx^2+(y-c)^2=r^2として考えていきます。
(1) P1, P2と1点ずつ共有するなら、P1と(0,0)のみで、P2と(0,m)のみで接することが分かります。そうなるようなa,b,c,r,mの条件を整理していきましょう。
(2)P1, P2と2点ずつ共有するなら、P1とCを連立してできるyの2次方程式と、P2とCを連立してできるyの2次方程式が、両方とも重解を持つはずです。このときに、その重解(つまり接点のy座標)がどんな条件を満たしていないといけないかに注意が必要です。
<筆者の解答>