みなさん、こんにちは。
今回は「シュレディンガー方程式」シリーズの第1弾「井戸型ポテンシャル」の後編で、「有限の深さ」になった場合について考えます。
前回の記事↓
1. 井戸型ポテンシャル(有限深さ)
井戸型ポテンシャルをおさらいすると、両側を壁に囲まれ粒子が閉じ込められてる状況でした。
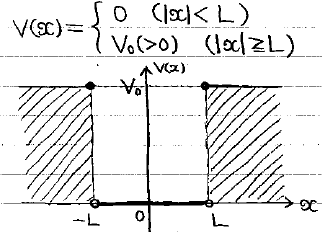
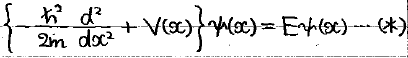
今回は、壁の高さがV0という有限の値である場合を考えます。
もし、粒子のエネルギーEがE>V0だとすると粒子は容易に壁を超えることができてしまうので、粒子が閉じ込められるE<V0となる状況を考えることにします。
1-1 一般解の導出
まず、壁の内側については前回と全く同じです。
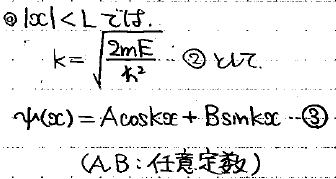
次に壁の外側については、指数関数を用いた一般解ができます。
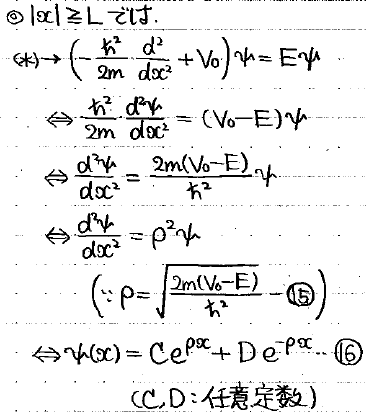
ρについてですが、E<V0を考えているのでルートの中身は正になります。
壁から無限に離れた場所には粒子は存在しえないので、x→±∞で波動関数は0になります。
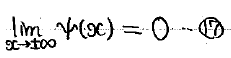
この性質から、壁の外側での波動関数は下のようになります。
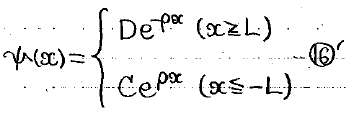
さらに、粒子の存在確率(=波動関数の2乗)はx=0で対称なので、波動関数は偶関数か奇関数となることが分かります。
1-2 境界条件
例のごとく、任意定数が残っているので、次のように境界条件を課します。
2. 粒子の存在確率の総和は1
1については「微分可能」というのが前回なかったポイントですね。2は前回と一緒ですが、今回は実はあまり重視せず「そうなるように任意定数を定める」程度に留めます。
まず、波動関数が偶関数の場合を調べると、1の条件から2つの式が決まります。

割り算してA,Cを消去すると、ρとkの関係式が求まります。
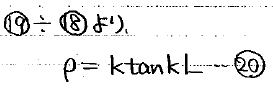
本当はここからEの値を求めたいのですが、Eについて綺麗に解けない方程式なのでEの形を直接調べることは諦めます。
両辺にLをかけると、kL、ρLを一まとめにして考えられます。
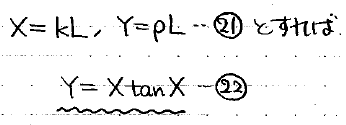
波動関数が奇関数の場合も同様です。

このとき、X^2+Y^2を計算するとEが綺麗に消えて定数になるので、関係式の一つとして「XY平面上の円」ができます。
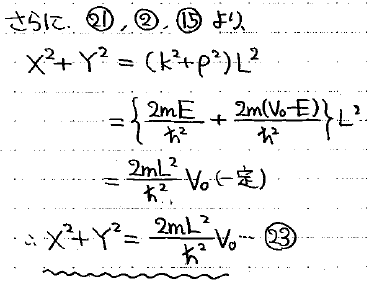
さらに、最終的に求まったXとYの2つの関係式を一まとめにすると下のような曲線になります(どちらか一方が成り立てばいいので、積=0を考えてあげれば表現できます)
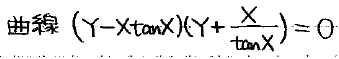
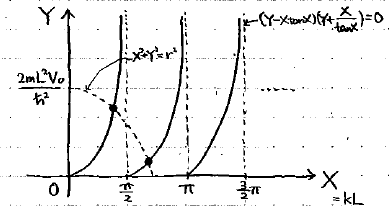
長くなりましたが、結局この円と曲線の交点に対応するEの値こそが、今回の粒子の固有エネルギーとなります。ここでも、エネルギーは飛び飛びになっています。
1-3 結果から言えること
さて、これで一通りの調査が終わったわけですが、一つ不思議な点があるはずです。
最初に「粒子は壁の内側に閉じ込められていて、壁を越えられない」という前提でE<V0を設定してシュレディンガー方程式を解いたはずでした。
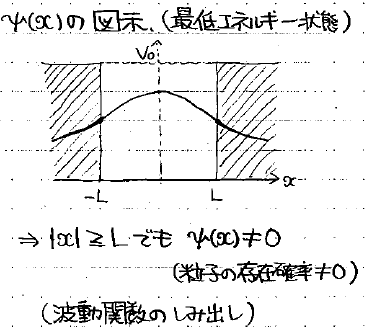
しかし、実際には壁の外側にも波動関数が存在しています。波動関数は粒子の存在確率なのですから、「壁よりも低いエネルギーしか持ってないはずの粒子が、壁の外側にも存在しうる(波動関数の染み出し)」という不思議な状況が起こっているのです!
これをマクロな話に置き換えると如何におかしな状況かが分かります。
普通であれば、人間は自分のジャンプ力以上の高さの壁を超えることは絶対にできません。しかし、上記の事実は、ジャンプ力が壁の高さより低くても壁の向こう側に行ける可能性がある。ということになります。
言い換えれば、「(ごく低確率ではあるが)壁をすり抜けられる」ということに他なりません。この現象は量子力学の言葉で「トンネル効果」と呼ばれます。
このように、ミクロの世界では通常では考えられない現象がいくつも起きうるのです。