皆さん、こんにちは。
今回は、複数のデータの組が与えられた時に、尤もらしい関数を求める「最小二乗法」について紹介します。
実は前回紹介した疑似逆行列も関連する話となっています。
係数行列に逆行列がないときにどう連立1次方程式を解く? ~疑似逆行列~ - ちょぴん先生の数学部屋 (hatenablog.com)
1. 最小二乗法
1-1. 最小二乗法とは?
最小二乗法とは、複数のデータの組があった時に、その関係を近似できる関数を求める手法です。
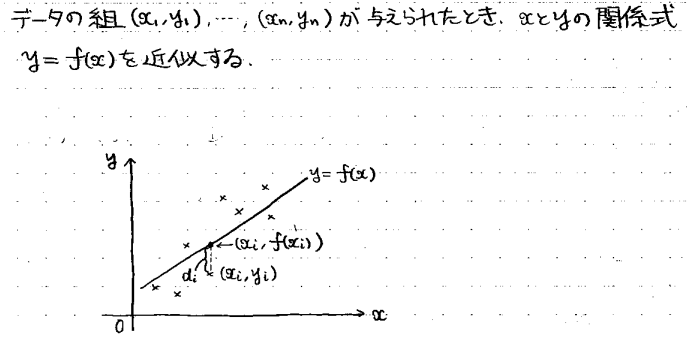
例えば、上の図のように×でいくつかデータをプロットしたときに、それを尤もらしく近似できる直線y=f(x)を求めるわけです。
このように、いくつかのデータから、尤もらしく近似できる式y=f(x)を作って、y=f(x)を使って予測をするという作業(回帰分析)は、今流行の「機械学習」の最も基礎的なものです。
AIにいくつかのデータを「学習」させて予測式を作ってもらい、その予測式を使って未知のデータに対する予測をしてもらうわけです。
さて、具体的にどのようにして尤もらしい関係式y=f(x)をつくるのか?
曲線と各データの間には当然誤差が乗ってきます。その誤差をdiとすると、
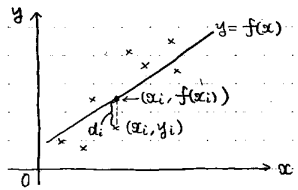
![]()
とかけます。
この誤差の合計が最も小さくなるようにf(x)を決めてあげれば、f(x)が尤もらしい近似式になると考えられるので、
次のような誤差の合計Dを最小化します。

diそのものの和を取らずに2乗してから和を取るのは、その方が計算が楽だからです。絶対値が入ったままだと数式の処理がしにくいので、本質を変えずに数式処理のしやすい形である2乗に置き換えています。
このように誤差の2乗の和を最小化するので「最小二乗法」という名前が付いているわけです。
1-2. 回帰直線
では、最小二乗法のなかで最も基本的で、最も広く使われる「f(x)を1次関数=直線で考えた場合」について考えていきます。
今、求めるf(x)の式を
![]()
として、

を最小にする係数α、βを求めます。
それには、αによる偏微分と、βによる偏微分が両方0であればOKです。

※偏微分についてはこちらで解説しています。
ラグランジュの未定乗数法 ~制約条件付きの最大最小を求める秘密兵器~ - ちょぴん先生の数学部屋 (hatenablog.com)
⑤を変形すると、

となります。
ここで、上にバーを付けた量はn個のデータの平均値です。
同様に⑥も変形すると、

となります。
⑤’と⑥’はαとβの連立1次方程式になっているので、逆行列を使って解くと、

となります。
ここで、平均以外の統計量、分散・共分散を定義しておきましょう。
xの分散は、各データの平均値からのズレの平均なので、

と計算できます。
共分散は、xの平均からのズレ、yの平均からのズレの積の平均なので、

と計算できます。
これと、xの平均とyの平均を、μで表現することにします。
![]()
これらを⑦に代入して整理すると、

αとβが、xとyの平均、分散、共分散といった基本的な統計量だけの式で計算できました。
よって、求めたかった直線y=f(x)の式は、

となります。
このようにして求まった直線を「回帰直線」と呼びます。
1-3. 回帰直線導出の具体例
それでは、ここで具体例を出しましょう。
とある9人組に数学と英語のテストを受けてもらった結果、結果が次のようになったとします。

(※どっかで見たことのあるような名前が並んでいますが、他意はありません笑)
数学の成績と英語の成績には相関がありそうなので、両者の回帰直線を求めてみたいと思います。
数学の平均点と標準偏差(=分散の平方根)、英語の平均点と標準偏差、両者の相関係数(=共分散÷標準偏差の積)を計算すると、

となっているので、
次のPythonプログラムで回帰直線を定義通りに求めると、

各係数が
![]()
と求まります。
回帰直線を求める機能はexcelにもあるので、そちらで回帰直線を求めると、

excelでの結果も同じ値になっていて、excelでも正しく回帰直線が計算できていることが分かります。
1-4. 行列での記述方法
さて、この最小二乗法ですが、行列の形で表現することができます。
今、回帰直線を求める場合について、次のように行列とベクトルを定義すると、

最小化したかった誤差の2乗の和Dは、

ベクトルのノルム(=大きさ)を使って表せます。
つまり、Dを最小化することは、
![]()
を最小化することと全く同じです。
これは、別に回帰直線に限ったことではありません。
例えば、説明変数が2つあって1次式で近似したい場合は

を最小化するわけですが、次のような行列・ベクトルを定義すると、

Dは、

やっぱり同じ形になります。
別の例として、2次以上のm次多項式で近似したい場合は、
(※mは、データの個数nよりも小さくとります)

を最小化するわけですが、

を定義すると、

やっぱり同じ形になります。
よって、最小二乗法は、
![]()
を最小にするようなベクトルxを求める問題と等価、ということが分かります。
2. 疑似逆行列を使った最小二乗法の解法
それでは、
![]()
を最小にするようなベクトルxをどうやって求めればよいのか?実はここで前回紹介した「疑似逆行列」が登場します。
係数行列に逆行列がないときにどう連立1次方程式を解く? ~疑似逆行列~ - ちょぴん先生の数学部屋 (hatenablog.com)
早速、定理を紹介します。

前回紹介した「最小ノルム解」では、Aの各「行」ベクトルが1次独立という条件でしたが、今回はAの各「列」ベクトルが1次独立という条件になります。
前者の場合はAは横長の行列になりましたが、後者の場合はAは縦長の行列です。
この定理の証明は3段階の証明になります。
第1段階は
![]()
の証明です(AとA†の順番が前回と逆になっていることに注意)。
証明の流れは前回とほぼ一緒なので、一気に掲載しちゃいます。


次の第2段階が、少しハードです。
![]()
ノルムを2乗にしたもの(つまりD)を計算すると、

となります。
このとき、この値を最小化したいので、ベクトルxで微分します。
ベクトルで微分するので、ベクトル解析の知識が必要になるのですが、ここでは、

で定義される演算子∇(ナブラ)を㉓の両辺に作用させて、その結果が0になるように検討します。
(※∇についてはこちらで解説しています。grad, div, rotとは? ~ベクトル解析の3大計算~ - ちょぴん先生の数学部屋 (hatenablog.com) ここでは、勾配gradを計算することになります)
まず、㉓の第2項に∇をかけてみましょう。すると、

となります。1次式axを微分するとaになることと似ていますね。
次に、㉓の第1項に∇をかけると、Bがエルミート行列なら、

となることが知られています。ax^2を微分すると2axになることと似ています。
今回の場合A†Aがエルミート行列なので、この公式が適用可能です。
公式を2×2行列の場合について証明すると次のような感じです。
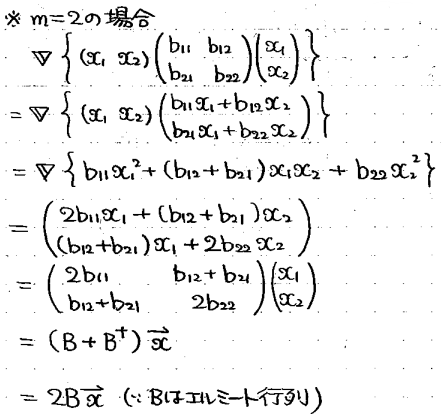
㉓の第3項はただの定数なので、微分すれば当然0です。
以上の結果をまとめると、

となり、この値が0になっていればいいので、

これで、第2段階の証明ができたことになります。
最後は、
![]()
を証明すればいいのですが、これは前回の「最小ノルム解」の第4段階とほぼ同じ証明方法なので、こちらも一気に掲載します。

以上から、最小二乗法の解の定理が証明完了です。
先ほどの例、

について、疑似逆行列を使う方法で回帰直線を求めてみましょう。
係数行列Aを作り、さらにその疑似逆行列を作るプログラムをPythonで実装すると次のようになります。
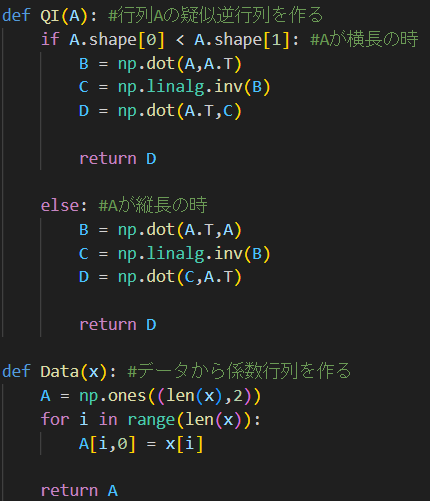
(※前回の「最小ノルム解」の場合の疑似逆行列も作れるようにしてあります)
係数行列Aを出力すると

という9×2行列となり、これの疑似逆行列を出力すると、

という2×9行列になります。
(改行が入って見にくくなってしまいすみません)
この結果を使って最小二乗法の解を

で計算すると、結果は、
![]()
となります。
これは、先ほどのexcelでの解

と確かに一致しています。