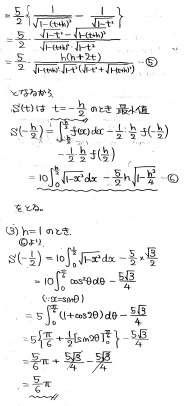このシリーズでは、東京医科歯科大学の数学の問題を解いていきます。
30回目の今回は1993年です。
第1問

1次変換についての問題です。背景には行列の「固有ベクトル」がある問題です。
この2次曲線の正体はな~んだ? ~行列の対角化~ - ちょぴん先生の数学部屋 (hatenablog.com)
(1)点(x,y)がfによって(x,y)に移る、という条件からx,yの条件を調べます。
(2)y=ax+b上の点(s, as+b)をfによって移動した点が、sによらずy=ax+b上にある、という条件からaとbを決定していきます。
(3)これは、「fがy=2xに対する対称移動を表す1次変換」だと気付けないと地獄を見ます。仮に「PとQの座標をパラメータ表示してPQを予選決勝法で最小化する」という作戦を思いついて実行しても、そもそも多項式と指数関数が入り混じった式になって微分がうまく処理できません。
では、どうやって「fがy=2xに対する対称移動を表す1次変換」に気付くか?その伏線こそが(1)と(2)です。
(2)の結果から、求まった2直線の方向ベクトル(1,2)と(-2,1)がfにとって特別な方向ではないかと予測でき、実際に(1,2)はfに対して不動で、(-2,1)はfによって(2,-1)に反転します。
この2つのベクトルは直交しているので、任意の点はα(1,2)+β(-2,1)と表現できます。それにfを噛ませてあげると、結果的にα(1,2)-β(-2,1)となって、「y=2xに平行な成分」についてはそのまま、「y=2xに垂直な成分」はちょうど逆向きになることが分かります。
この事実に気付ければ、PQの最小値は、結局Pとy=2xの距離の最小値を考えればよいと分かるわけです。
<筆者の解答>


第2問

集合を絡めた整数問題です。
(1)各位の和が3の倍数になることが、Zに含まれる条件です。そのような整数は、(1,1,2,2)を並び替えたものしかないことが分かります。
(2) 1をa個、2をb個、4をc個使うとして、合計が3の倍数になるような(a,b,c)の組を調べていきます。cの値で場合分けすると見通しが良いです。
(3) 求めるxが「pqrs」と書けるとして、p+q+2r+2sが3の倍数になるように(p,q,r,s)を決めていきます。
(4)(5)
(3)の結果を利用するとよいでしょう。(3)の答えの中に1111が含まれているので、Aの要素の1つを1122とできます( (5)を見越すとこうしたほうが楽です)。
残りの2つの要素は(3)の答えの残り5つから選んでいきます。このとき1122との積が3の倍数になることは保証されているので、次に1111との積が3の倍数になるものを選び、さらにどの積も3の倍数となるように選んでいきます。
<筆者の解答>


第3問

楕円の面積の増減に関する問題です。
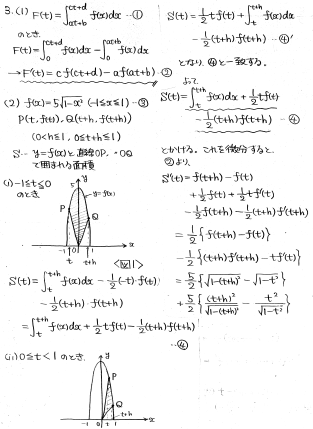
(1)積分区間を中身に突っ込むパターンです。積分区間その物の微分をかける必要があることに注意です。
(2)図を描いてSの式を調べることが先決です。Pの位置によって場合分けが起きますが、結局同じ式にまとめられます。その後(1)の結果を使いつつ微分して、S'=0になる瞬間を調べます。
結果は、PとQがy軸について対称な時に、Sは最小となります。
(3)
(2)の結果に代入して積分計算を実行すればOKです。
<筆者の解答>