皆さん、こんにちは。
今回は、大学入試でもしばしば出てくる、
「実数x,yが、x^2 +y^2 =1を満たしながら動くとき、f(x,y)=xyの最大値と最小値を求めよ」
のような類の問題を、大学で習う秘密兵器を使って解く方法を紹介します。
その名も、「ラグランジュの未定乗数法」といいます。
1. 偏微分について
まず、「偏微分」の知識が必要なので、これについて解説します。
偏微分とは、「2つ以上の変数を持つ関数を、ある特定の変数についてだけ微分すること」です。
具体例を挙げましょう。
xとyの関数f(x,y)が以下のような場合、

fの「xによる偏微分」は、yを定数と見なしてxで微分すればいいので

となります。(※偏微分は、上のような特殊な表記の仕方をします)
同様に、fの「yによる偏微分」は、xを定数と見なしてyで微分すればいいので

となるわけです。
さて、この偏微分がどういう場面で登場するのか?以下のような問題を考えてみます。
「曲面z=1- x^2 - y^2 の、点P(s,t, 1 - s^2 - t^2)における接平面αの式を求めよ」
接平面とは、2次元平面における接線の3次元バージョンと考えればOKです。
状況を図にすると下のような感じです。

接平面αの式は、一般に

とかけるので、このαと曲面z=f(x,y)が、点Pだけを交点に持つようにa,b,cを決めてあげましょう。両者の式を連立すると、
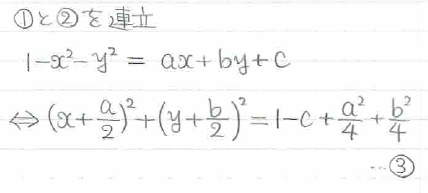
となります。③をみたす(x,y)の組が1組だけになるには、③の右辺が0になればOKですね。よって、求める条件は、

となって、a,b,cを全部計算すると、

となります。これを使って改めてαの式を書くと、

となりました。
ここで、xとyの係数に注目すると、それぞれ「xについての偏微分」「yについての偏微分」に点Pの座標を代入したものになっています!これは、今回の例に限らず一般的に成り立ちます。
そして、平面αの法線ベクトルは(a,b,-1)とかけるのでした。
以上を総合すると、偏微分の値を並べたベクトル

は、接平面αの法線ベクトル(の水平成分)となることが分かります。
2. ラグランジュの未定乗数法
まず、「ラグランジュの未定乗数法」とはどんな方法なのか、結論から言います。

偏微分を使うことで、「制約条件の下で」2変数以上の関数の極値を計算できるというものです。(厳密には極値の候補です)
一般に上にあるg(x,y)=0のことを「制約条件」と呼びます。
最大最小にしたい関数f(x,y)をそのまま偏微分するのではなく、よく分からないλという数を持ってきて制約条件g(x,y)=0 と絡めて、「f-λg」を偏微分する、という一見するとよく分かんない作業をしています。
(※制約条件がない場合はg=0にすればよく、素直にf(x,y)をそれぞれ偏微分すればいいことになります)
なんでこんな変な作業をするのか?直感的に理解する方法を説明します。
今、簡単のために、曲面z=f(x,y)を山だと思って下さい。山に作られた登山道(赤線)をxy平面におろした曲線をg(x,y)=0だと思って下さい。

この登山道の中で一番低い場所と一番高い場所を求めて下さい、というのが今回の問題です。
この山を上から見て、等高線(青線)を引いてみましょう。

一番内側にある等高線は、明らかに登山道よりも標高が高い位置になります。そこから徐々に等高線の標高を下げていきます。
すると、ある標高で等高線と登山道が接する場面が登場します(図の濃青線)。登山道の、等高線との接点以外の部分は、接点の標高よりも低い位置にあることになります。
ということは、この接点こそが「標高が一番高い場所=最大値」と言えそうです。
等高線と登山道が接するということは、両者は共通の接線(紫線)を持つはずです。
共通の接線を持つということは、接点における「等高線の法線ベクトル」と「登山道の法線ベクトル」が同じ向き(あるいは逆向き)になるという事です。
これを式にすると、「等高線の法線ベクトル」=「登山道の法線ベクトル」の定数倍ということなので、先ほどの偏微分の知見を使えば、

となるわけです。右辺を左辺に移項すれば、

となって、確かに、f-λgを偏微分すればいいんだと分かります。
3. 例題
さて、ここで例題を一つ解いてみましょう。この記事の冒頭に書いた、

です。
高校数学の範囲では「パラメータ表示を使う」「円と双曲線が接する条件を考える」などの解法で解くことができ、いずれの場合も最大値1/2, 最小値-1/2が求まります。

この問題を、今回紹介した「ラグランジュの未定乗数法」で解いてみます。
目的関数f(x,y)を

制約条件g(x,y)=0を

とすればいいので、定数λを使って

を同時に満たすような(x,y)を探していけばよいわけです。この連立方程式を行列の形で書くと、

となるので、行列式が0になるか否かで場合分けが発生します。
まず行列式が0にならない場合から検討すると、この時はx=y=0と求まりますが、これはそもそも制約条件をクリアしていないので不適です。

次に、行列式が0になる場合は、x=y, x+y=0という2種類の関係式が求まり、これと制約条件を連立すれば(x,y)、ひいては極大値と極小値が求まります。

今回の制約条件は円であり、「不連続な点や尖った点、端っこの点(これらを特異点と言います)」などが存在しないので、上記で求まった極大値極小値がそのまま最大値最小値になります。

このようにして、高校数学の解法と全く同じ答えが出てきます。
もし、制約条件の中に「不連続な点や尖った点、端っこの点」といった特異点がある場合は、例外扱いで個別にf(x,y)の値を計算する必要があります。

4. 京大2012年理文共通第3問を「ラグランジュの未定乗数法」で解く
それでは、大学入試の過去問を、ラグランジュの未定乗数法で解いてみましょう。
今回取り上げる問題は、京都大学の2012年に出題された、下記の理文共通問題です。

※高校数学での解法は以下の記事で紹介しています。
平成の京大理系数学 -2012年- - ちょぴん先生の数学部屋
この問題は、「とある制約条件の下でxとyの関数の最大値最小値を求める」という、まさにラグランジュの未定乗数法が使える問題となっています。
最初に、愚直に適用した解法を紹介します。
目的関数f(x,y)と制約条件g(x,y)=0を以下のように定義し、

定数λを使った以下の関数F(x,y),
![]()
を偏微分していくことになります。すると以下のようになります。

これを連立して解くのはかなり骨が折れそうです。しかし、同じ項がいくつか含まれているので、⑤と⑥を引き算すれば光が見えてきそうです。実際にやってみると、

といった具合に、2種類の関係式が求まります。それぞれについて検討していきます。
まず簡単な前半の式については、制約条件を使うと下のようになります。

これがf(x,y)の極値候補のその1です。
後半の式については、対象式の性質をうまく使ってλだけの方程式にすると見通しよく解くことができます。



λが2種類求まったので、それぞれ検討すると、極値候補が2つ求まります。

これら、極値候補の3種類の座標それぞれについてf(x,y)の値を計算して大小比較してあげれば下のようになります。




最後に、制約条件、
![]()
に特異点があるかどうかをチェックしますが、実はこの式、以前「行列の対角化」の記事で取り上げた通り「楕円」を表す式なので、特異点はありません。
以上から、f(x,y)の最大値と最小値が求まったので、

が分かりました!これは、高校数学で解いた答えと全く一緒です。
次に、目的関数と制約条件の両方が「xとyの対称式」となっていることを生かした解法を紹介します。
まず、
![]()
と変数変換を行います。xとyが実数でないといけないので、
![]()
という条件が追加されます。
この変数変換を行ったうえで、目的関数f(s,t)と制約条件g(s,t)を以下のように定義し、

定数λを使った以下の関数F(s,t)
![]()
を偏微分します。すると、

となります。先ほどの変数変換せずに愚直に解いた場合よりもかなり式が簡単になっています。②と③と④を連立すると、

とsが2種類求まり、それぞれ検討すれば、

と、極値候補が求まります。
最後に、制約条件の特異点を考えます。
今回の制約条件は、
![]()
![]()
の2つの式を同時に満たすので、st平面上に描くと下の太線のようになります。

今回の場合は、制約条件に「端っこの点=特異点」が存在しています!なので、この端点を個別に考えないといけません。
3次元空間で描くと下のようなイメージです。

特異点におけるf(s,t)の値を考えると、

となります。
以上4つの値が出揃ったので、同じように大小比較をして、

と同じ答えが求まります!
5. 最後に
このように、制約条件付きの最大最小を考えるうえで、「ラグランジュの未定乗数法」は機械的に解くことのできる秘密兵器だったわけです。
大学入試では、当然ながら「対称式で簡単にできる」とか「パラメータ表示できる」とか「グラフの問題に帰着できる」とか高校数学の範囲で解ける問題しか基本的には出題されませんは、うまい解法が思いつかなかった時の最後の手段として、この「ラグランジュの未定乗数法」を知っておくと役立つかもしれません。