このシリーズでは、山梨大学医学部後期の数学の問題を解いていきます。
5回目の今回は2018年です。
第1問(1)
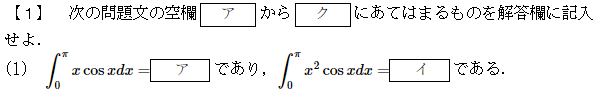
積分の計算問題です。
定石通りに部分積分を行えばよいでしょう。x^2やxが消えるように部分積分していきます。
<筆者の解答>
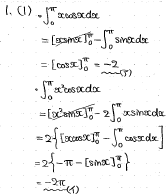
第1問(2)
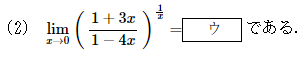
極限の計算問題です。
このままでは1^∞の不定形になってしまいますが、この形を見た瞬間にネイピア数eの定義を連想してほしい所です。括弧の中身を1+△の形にし、指数の肩を1/△になるように辻褄を合わせていきます。
<筆者の解答>
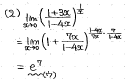
第1問(3)
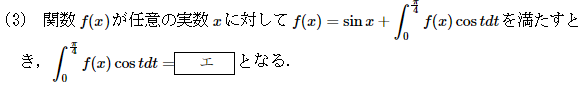
(訂正:積分の中身はf(x)ではなくf(t) )
積分方程式の問題です。
エ=Aとおいて、f(x)を代入することでAを求めていく典型問題です。
<筆者の解答>

第1問(4)
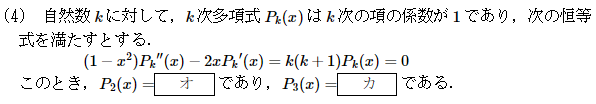
(訂正:k(k+1)の前は=ではなく+)
微分方程式に関する問題です。
オについてはP2(x)=x^2+ax+b, カについてはP3(x)=x^3+px^2+qx+rとおいて微分方程式に代入して、それがxの恒等式になるように係数を決めていけばよいでしょう。
ちなみに、この微分方程式は有名な方程式で「ルジャンドルの微分方程式」と呼ばれています。そして、この方程式を満たす多項式の事を「ルジャンドル多項式」と呼びます。つまり、今回の問題は、2次と3次のルジャンドル多項式を求める問題だったわけです。
このルジャンドルの微分方程式は量子力学の分野で登場し、特に「水素原子のシュレディンガー方程式」を解く際に登場してきます。
<筆者の解答>

第1問(5)

平面に対する対称移動に関する問題です。
αの式を求めることでαの法線ベクトルnがわかり、ODベクトルはnの定数倍になります。ODの中点がα上にあることからその定数が求まることになります。
△OCDの面積は公式をそのまま使えばよいです。
<筆者の解答>

第2問(1)

制約条件がある下での目的関数の最大最小を考える問題です。これは高校数学の範囲ではなかなかの難問ですね。
1つの方法は「制約条件をy=の形に直して、目的関数をxだけの式に直す」というものがあり得ますが、式が非常に汚くなるうえにy=の時点で2通りの表気が出てくるので場合分けも発生し、手に負えないでしょうね。
目的関数が対称式なら、全部をs=x+y, t=xyの式に変換するという方法も取れたと思いますが、今回は残念ながら目的関数が対称式ではありません。
ここは、制約条件x^2+xy+y^2=1を満たすようにx,yをパラメータ表示するという方法を考えることにします。
この条件を満たす(x,y)を原点の周りに45°回転した座標(X,Y)を考えると、(X,Y)が楕円を描くので、XとYをパラメータθを使って表現できます。それを元に戻してあげればx,yがパラメータθで表現できることになります。
ここまでくれば、目的関数x^2+2xyをθだけの式で表現でき、しかも三角関数の合成を使えば微分要らずで最大最小が分かってしまいます。
この手の「制約条件が付いた目的関数の最大最小」を考える問題は、大学で習う「ラグランジュの未定乗数法」を使うと、機械的に比較的簡単に解くことができます。その別解も紹介していますので、ご参考までに。
※ラグランジュの未定乗数法については、以下で解説しています。
ラグランジュの未定乗数法 ~制約条件付きの最大最小を求める秘密兵器~ - ちょぴん先生の数学部屋 (hatenablog.com)
<筆者の解答>

※ラグランジュの未定乗数法を使った別解です。

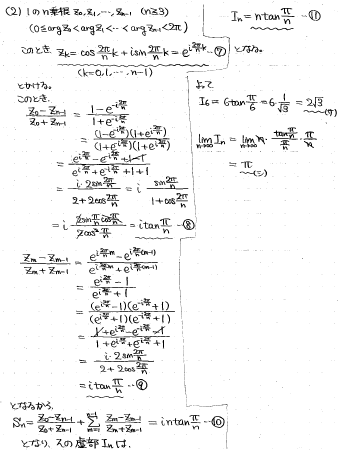
第2問(2)

複素数の計算問題です。
zk=cos(2πk/n)+isin(2πk/n)とすれば問題文の条件を満たすので、Snの各項を計算していけばよいでしょう。するとSnはシンプルな式になり、極限はsinx/x→1(x→0)を利用すると計算できる形になっています。
(※計算しやすくなるように、答案では大学範囲ですが「オイラーの公式」を使っています。オイラーの公式についてはこちらの記事を参照数学界のKingとQueenは、愛で結ばれた・・~世界で一番美しい数式、オイラーの等式~ - ちょぴん先生の数学部屋 (hatenablog.com))
<筆者の解答>
第2問(3)
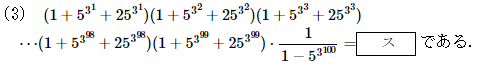
発想力が要求される計算問題です。
登場する数字がどれもこれもバカでかいですが、左辺の各因数が、x^3 -1=(x-1)(x^2+x+1)を連想させる形になっていることに気付ければ勝ちです。
分母分子にx-1に相当する数をかけてしまえば式を簡単にできます。
<筆者の解答>
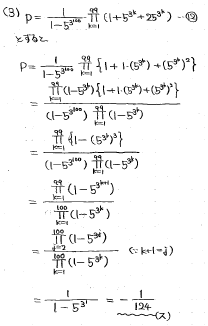
第3問

確率の問題です。
Aがk点とる確率と、Bがl点とる確率をそれぞれ計算して、それを使ってk>lとなる確率を場合分けして計算していく、という流れです。
やることは単純なのですが、とにかく長いの一言です。
<筆者の解答>


第4問

複素数平面の問題です。
Aについては、z+z*が「zの実部の2倍」であることに注意すれば、「単位円の外側で、かつ実部が0以上1/2以下になるz」を図示すればよいことになります。
Bについては、w=-1/zとおいて、Aにおけるzの条件式をwの条件式に書き換えてあげます。考えに詰まったらw=x+iyと書き換えてあげることで見通しが良くなると思います。
<筆者の解答>

第5問

曲線の長さを計算する問題です。
(1)公式の通りに積分計算していくのみです。
(2)Aでの法線の傾きが分かってしまえば、図形的にx1-x0とy1-y0の式を調べることができます。こうすることで計算量を節約できます。
(3) √{(dx1/dx0)^2+(dy1/dx0)^2 }をx0で積分していくので、この積分の中身の関数を計算することに尽きます。
<筆者の解答>


第6問
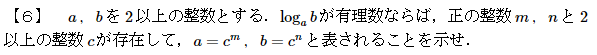
対数を題材にした整数問題です。
loga(b)が有理数なら、loga(b)=p/q (p,q: 互いに素な自然数)とかけて、この式を変形すると、a^p=b^qとなります。
このあとは、a,bの最大公約数dを考えることで、「互いに素」「分数=整数の形の等式」などを駆使してa,b,dの条件を詰めていきます。
<筆者の解答>
