皆さん、こんにちは。まだまだ寒いですね。
大学1年の後期の期末試験が近いということで、「電磁気学」に関連する数学の話を前後編に分けてしていこうと思います。
前編の今回は、電磁気学の基礎方程式である「マクスウェル方程式」の理解に必要な、ベクトル解析の諸計算について取り上げます。
※この記事では、「偏微分」については既知のものとして扱います。
0. ベクトル解析とは?
それを念頭に置くと、「ベクトル解析」とは、「ベクトルについての微分積分」ということになります。
今回の記事では、このうちベクトルの「微分」を行う、3つの代表的な計算grad, div, rotを紹介し、関連して「ラプラシアン」という概念も紹介します。
以後、x,y,zは、空間デカルト座標を表現するものとします(要するに、極座標ではない普通の座標です)
1. grad (勾配)
1つ目は、''grad''という計算です。日本語では「勾配」と呼ばれ、英語のgradientの頭文字です。
この計算は、「スカラー量をx,y,zでそれぞれ偏微分し、ベクトルの成分として並べる」計算となり、具体的には下のようになります。

いわば、fという3変数関数の、x方向の傾き、y方向の傾き、z方向の傾きをそれぞれ計算しているものとなっており、これが「勾配」と呼ばれる所以です。
物理では、「ポテンシャルエネルギー」を定義するときに使われたりします。例えば、位置エネルギーのgradを計算すると重力になる、といった具合です。

2. div (発散)
2つ目は、''div''という計算です。日本語では「発散」「湧き出し」などと呼ばれ、英語のdivergenceの頭文字です。
この計算は、「ベクトルのx成分をxで偏微分、y成分をyで偏微分、z成分をzで偏微分、したものを合計する」というもので、具体的には下のようになります。

これが何故「湧き出し」と呼ばれるのかは、以下のように説明されます。
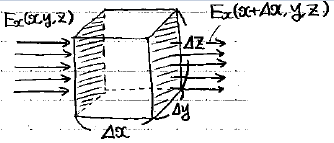
図のように各辺の長さがΔx,Δy,Δzの非常に小さい直方体を考え、それを水の中に漬けます。「単位面積当たりの」水の流量がベクトルE(x,y,z)で表されたとして、このとき、直方体の通過前後で流量がどれだけ変化するかを考えていきます。
簡単のためにx方向の流れのみに着目すると、流量変化は、(Eのx成分の変化)×(ΔyΔz)となり、今Δxが非常に小さいので、Eのx成分の変化は、Eのx成分のx偏微分×Δxと書けます。以上を総合すると、x方向の流量変化は、(Eのx成分のx偏微分)×ΔxΔyΔzと書けます。

y方向の流量変化とz方向の流量変化も同様に計算できるので、結局、直方体の通過前後の流量変化は、
(Eのx成分のx偏微分+Eのy成分のy偏微分+Eのz成分のz偏微分)×ΔxΔyΔz
=divE ×ΔxΔyΔz
となります。
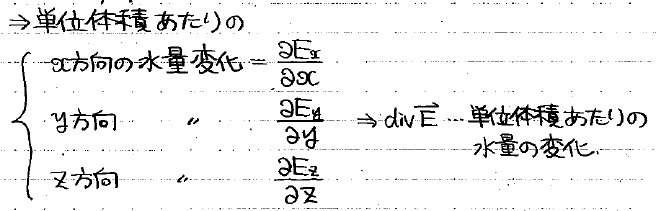
つまり、divEは、「単位体積当たりの」流量変化を表すことが分かります。
もしこの量が正であれば「通過前後で流量が増えている=直方体から水が湧き出している」、負であれば「通過前後で流量が減っている=直方体に水が吸い込まれている」と解釈できます。
これが、divが「湧き出し」と呼ばれる理由です。
3. rot (回転)
3つ目は、''rot''という計算です。日本語では「回転」と呼ばれ、英語のrotationの頭文字です。
この計算は、口で説明するのが難しいので、いきなり計算式を出しちゃいます。

gradやdivに比べると一段と複雑な計算です。何をやっているのかを以下説明します。
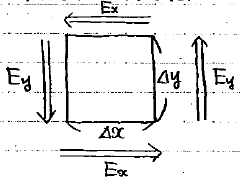
xy平面内に、縦横の長さがΔx, Δyの非常に小さい長方形を作り、その周りに渦を巻くように回転するベクトルEが存在すると考えます。
この長方形の各辺に沿って、その辺と平行なEの成分を積分し一周させると、結果
(rotEのz成分)×ΔxΔyと書けることが分かります。


x成分とy成分に関しても同様なので、結局rotEは、「Eの回転度合い」を表す量になっていることが分かります。
以上3つが、基本的な「ベクトルの微分」に関する計算手法なのですが、これは
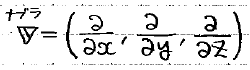
というベクトル∇を定義すると、(※∇は「ナブラ」と読む)

このように、gradは「スカラー量と∇の積」、divは「ベクトルと∇の内積」、rotは「ベクトルと∇の外積」という形にスッキリと定義できます。
4. ラプラシアン
(※演算子:d/dx(xで微分する)のような、操作を表す記号の事)
これはgradとdivを連続して行う、という操作を表す演算子で、下のように簡単に表現できます。

ラプラシアンは、後編の方で説明する「波の微分方程式」や、後日紹介しますが量子力学の「シュレディンガー方程式」などにも登場する、物理の分野では頻繁に登場する演算子です。
このラプラシアンに関連した公式を一つ紹介します。

この公式は次のように力づくで導出することが可能で、後編で紹介するマクスウェル方程式を電磁波の方程式に変形する際に使用します。

これで準備が整ったので、後編ではいよいよ「マクスウェル方程式」について考えていきます。