このシリーズでは、平成の北大理系数学の後期入試の問題を1年ずつ遡って解いていきます。
15回目の今回は2005年になります。
第1問

分数式が整数になる条件を考える問題です。
(1) m/(m^2 -m-1)はmを大きくするといくらでも0に向かって小さくなるので、1/|p|より小さくできます。すると、pが0でないとすると与式は整数でなくなってしまいます。
(2) f(m)をm^2 -m-1で割り算すれば、2次式+(1)の分数式、の形になります。m=0を代入したときも整数でないといけないのでaが整数でないといけないと分かります。すると(1)の結果を利用できます。
<筆者の解答>

第2問

不等式証明と関数の増減を調べる問題です。
(1) 両辺にxをかけた上で、左辺ー右辺の符号を微分を使って調べましょう。
(2) F(x)/xを微分すると、(1)の不等式を利用して符号の判断ができます。
<筆者の解答>

第3問

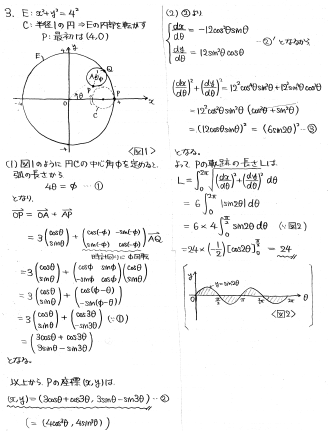
いわゆる内サイクロイドに関する問題です。
(1) Cの弧の長さとEの弧の長さが等しくなることに注目して計算していきます。
(2) (1)の結果をθで微分して計算していきますが、途中で絶対値が登場します。y=sin2θのグラフを思い起こすと絶対値を外すことができます。
<筆者の解答>
第4問

四面体の性質を証明する問題です。
最初、ベクトルの内積を利用してガンガン計算しようと思ったのですが、計算が手に負えないレベルになったので、方針転換しました。
ここは、AB⊥CDを生かせるように、ABをz軸上に、CDをxy平面上に置き、なおかつz軸周りに回転させることでCDをx軸に平行にすることができます。
このように座標系を設定すれば、平面BCDの法線ベクトルが求まり、垂線の満たす関係式が求まります。
あとは、2本の垂線に交点があるかを確かめれば終了です。
<筆者の解答>
