今日行われた2022年度共通テストの問題を見ていきます。
次に数学ⅡBを扱います。
※試験当日に解いており、ミスがあるかもしれません。
<略解>

[1/17追記] 第4問の(2)にミスがありました。
正しくは、サは4, シ~セは137です。申し訳ありませんでした。
<個別解説>
第1問[1]


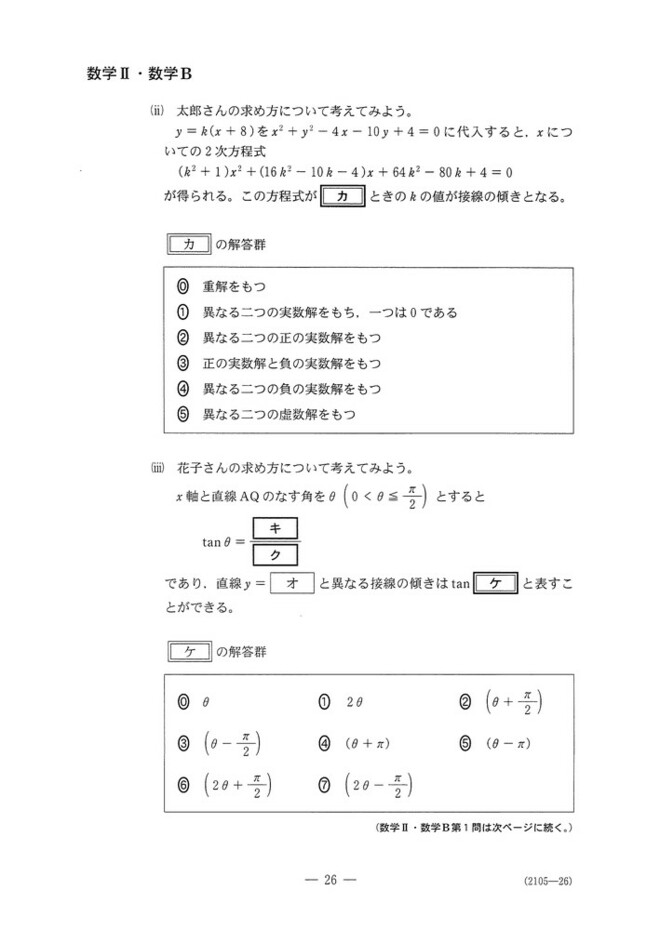

円と直線の共有点に関する問題です。
(1)Dの式を平方完成してあげれば中心と半径が分かります。不等号の向きから、周と内部なのは明らかでしょう。
(2)
(i)図を描くとCはx軸に接していることが分かるので、接線の一つがy=0であることはすぐにわかります。
(ii)Cとlの式を連立した方程式が重解を持てば、lはCの接線です。
(iii)AQの傾きがtanθであり、円の性質から、接線の傾きはtan2θになります。
(iv)k0はどっちの方法でも求まりますが、おそらく(iii)の方が楽です。視覚的に、Dとlが共有点を持つのが0≦k≦k0のときなことはすぐに分かります。
<筆者の回答>

第1問[2]


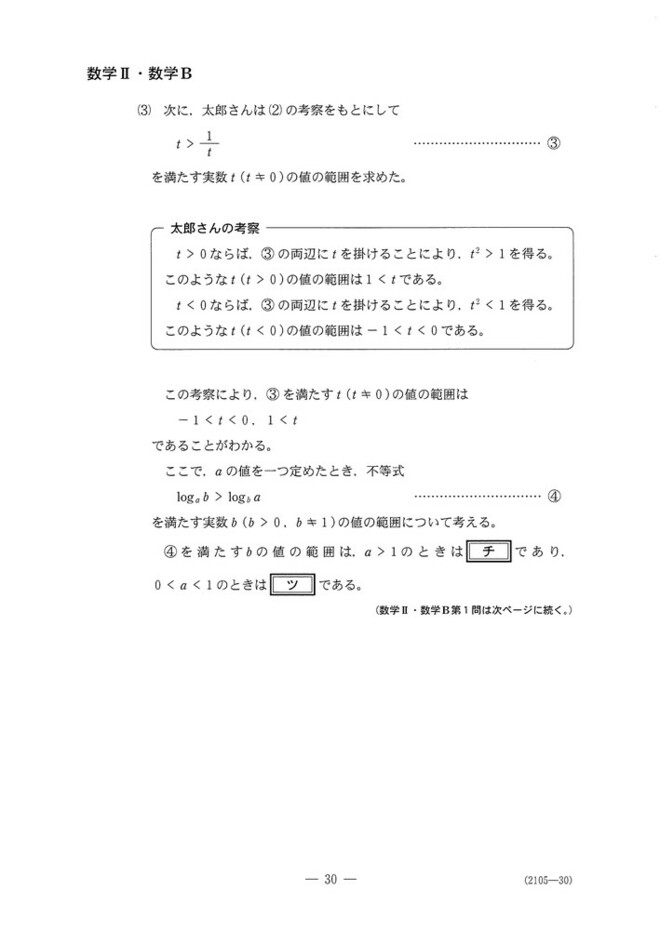

対数の大小を考える問題です。
(1)対数の定義に従って計算するだけです。
(2)対数の式を、定義通りに指数の式に書き換えるだけです。
(3)a>1のときはlogは増加関数、0<a<1のときは減少関数になることに注意します。
(4) p<1 ,q>1, r>1に注意して、(3)で求めた不等式が成り立つかを確かめましょう。a=pとして考えると速いです。
<筆者の回答>

第2問[1]
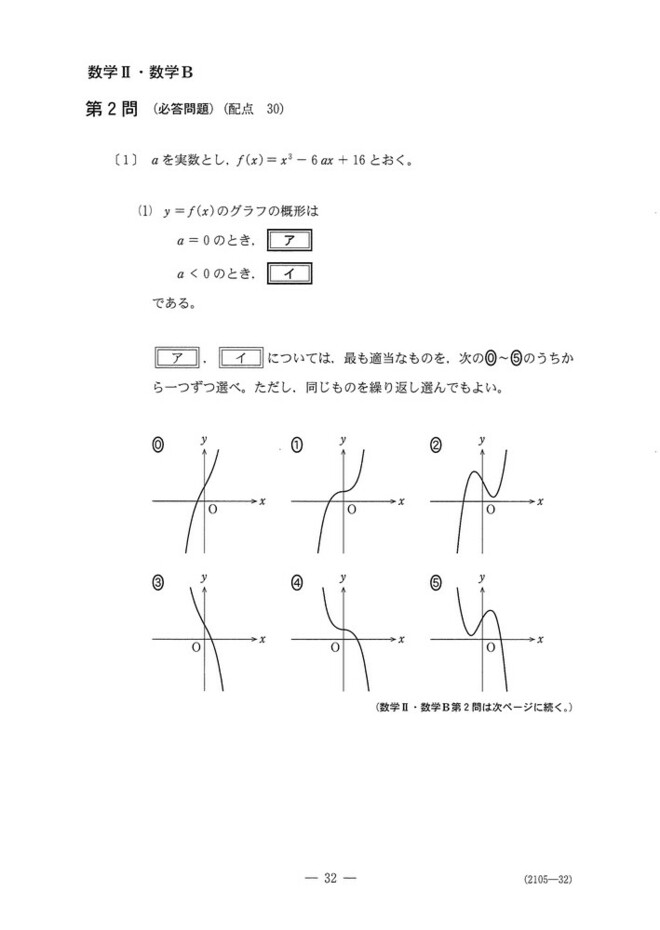

3次関数の増減の問題です。
(1) f(x)を微分すると、a≦0ならf(x)が単調増加なことが分かりますが、a=0のときだけf'(x)=0になる瞬間があることに注意しましょう。
(2) a>0ならf(x)は極値を持つので、y=f(x)のグラフを描いてしまえば一目瞭然でしょう。
pが極小値と一致するときは、f(x)=pの解の1つは重解で既に分かっているので、もう1個の解を調べましょう。
(3) aで場合分けして解の個数を数えます。極大値>0は明らかなので、極小値の正負に注目するとよいです。その上で論理関係に注意して解答してください。
<筆者の回答>

第2問[2]
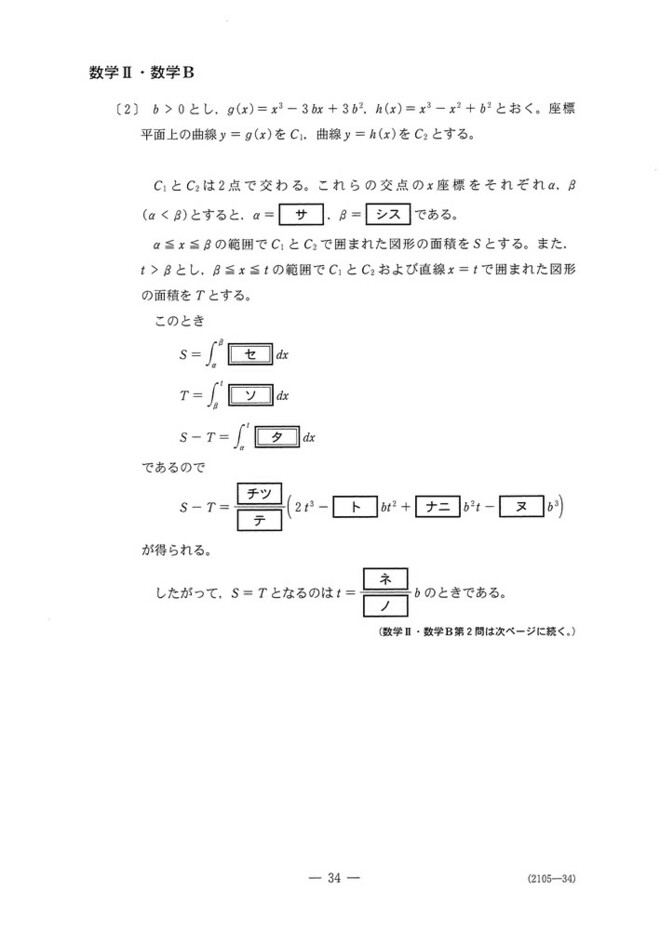

3次関数の積分計算の問題です。
g(x)=h(x)でα,βが求まり、その方程式からα≦x≦βではh(x)≧g(x)となっていて、それ以外の場所ではg(x)>h(x)となっていることが分かります。
それに注意して積分計算を進めます。計算ミスがない様に、αを代入すると0になるように積分の中身を工夫するとよいでしょう。
<筆者の回答>

第3問


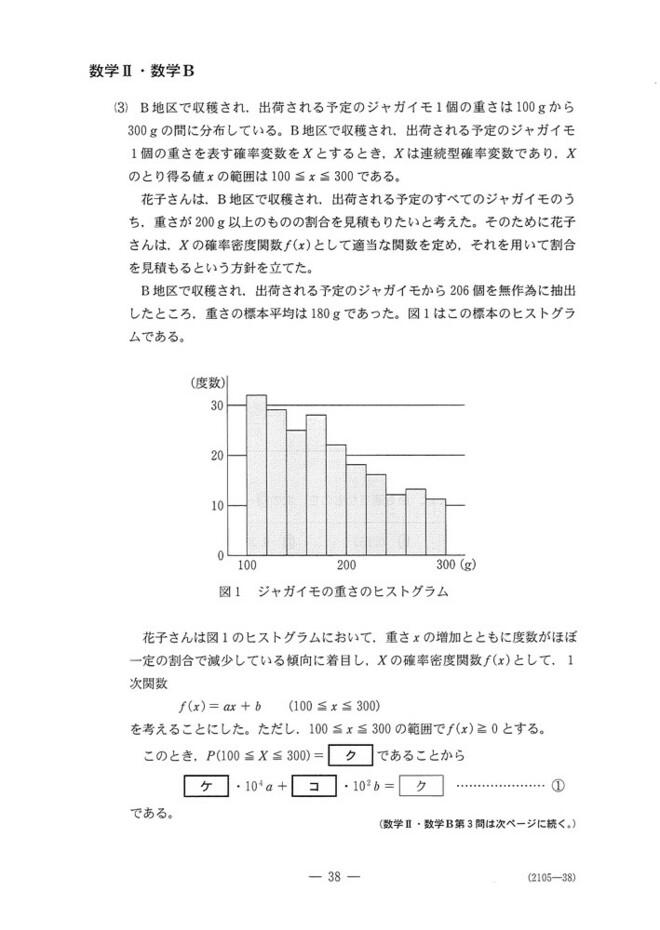

統計学の問題です。これを選択した受験生は少ないと思いますが、一応解説します。
(1) 200g以上である確率が25%, 200g未満である確率が75%で、サンプル数400なので、200g以上のイモの個数Zは、p=0.25, N=400の2項分布に従います。
2項分布に従う確率変数の平均値は、Npで求まります。
(2)Rの平均と標準偏差は、Zの平均と標準偏差をそれぞれ400で割ったものになります。
2項分布に従う確率変数の標準偏差は、√{Np(1-p)}で求まります。
正規分布表を使うときには、確率変数をX=(R-m)/σ (m:平均、σ:標準偏差)と変えてあげるとよいです。このときXは平均0, 標準偏差1の「標準正規分布」に従います。
(3) 確率密度関数f(x)を全区間で積分すれば値は1になるので、それを利用すればケコが求まります。あとはmの式と連立してあげればa,bが求まります。
200g以上の割合は、f(x)を200≦x≦300で積分してあげればOKです。
<筆者の回答>

第4問

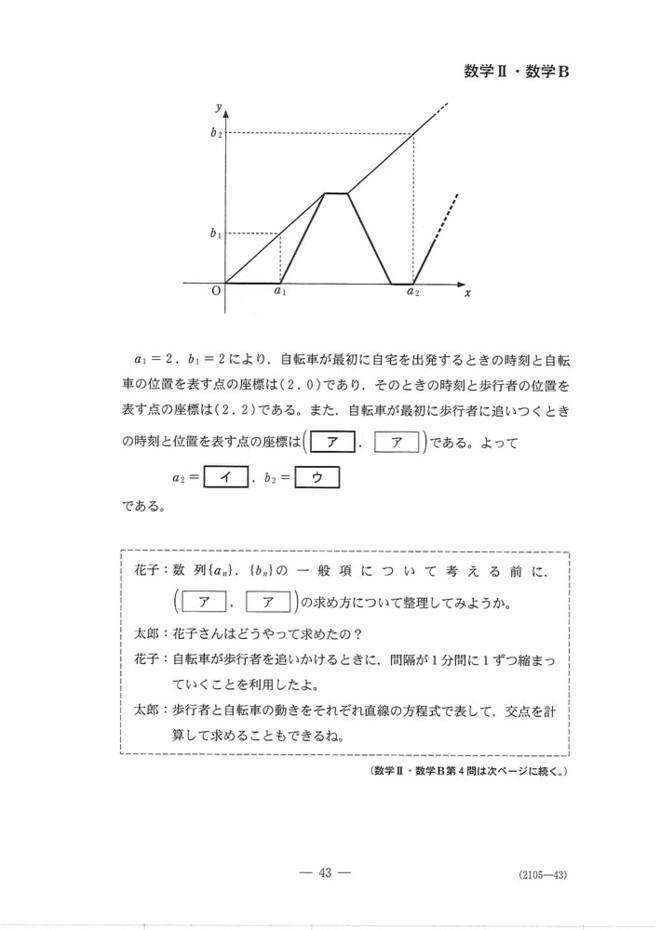
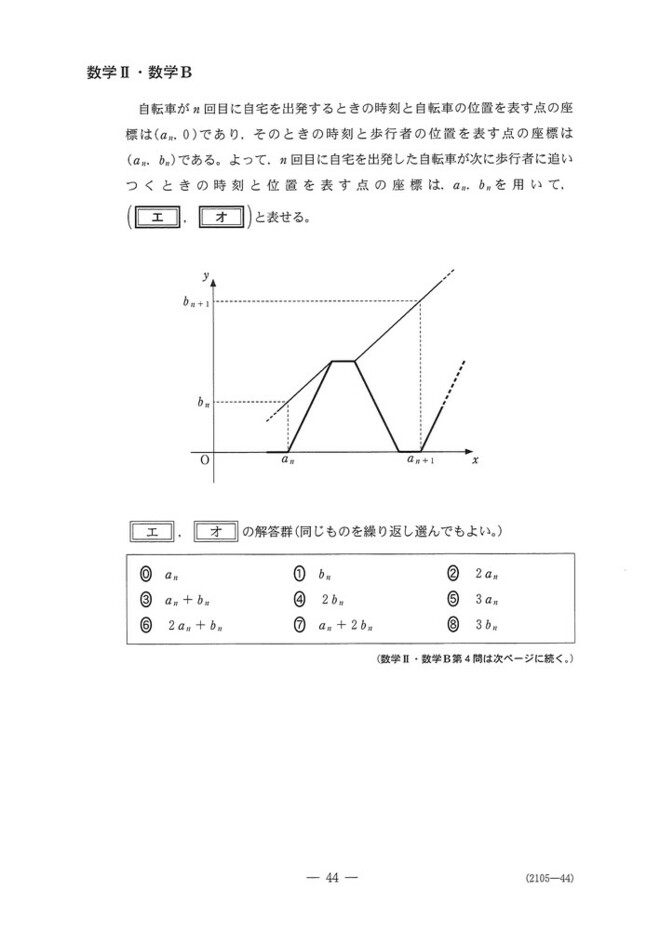
人と自転車が往復して・・・という題材を使った数列の漸化式の問題です。忘れ物を何度も取りに行って逐一渡しているような状況を想定しているんですかね笑(忘れ物し過ぎだと思いますけど)
(1)最初の1回目は実際に数直線を書いて実験してみるとよいです。
一般のn回目は、問題文にあるグラフを利用して考えます。(エ、オ)は、(an,0)を通る傾き2の直線と、(an,bn)を通る傾き1の直線の交点になるので、連立方程式で求めます。
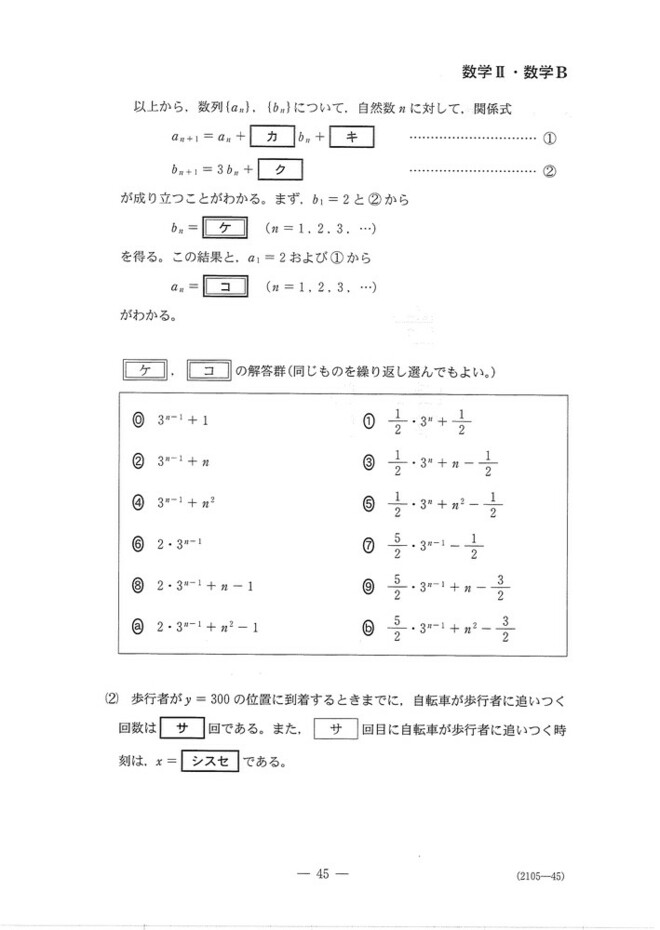
これを利用すると、グラフからanとbnの漸化式が立ちます。
bnについては標準的な特性方程式を使って解くパターンですし、anは、bnの一般項を入れれば階差数列の形に出来ます。
(2) bn≦300となるnの最大値を考えてあげればよいでしょう。シ~セは、(エ、オ)を利用すると求まります。
[訂正]正しくは、2bn≦300となるnの最大値です。すみませんでした。
<筆者の回答>

※(2)の答案を訂正します。

※以下、初稿で上げた誤答です

第5問
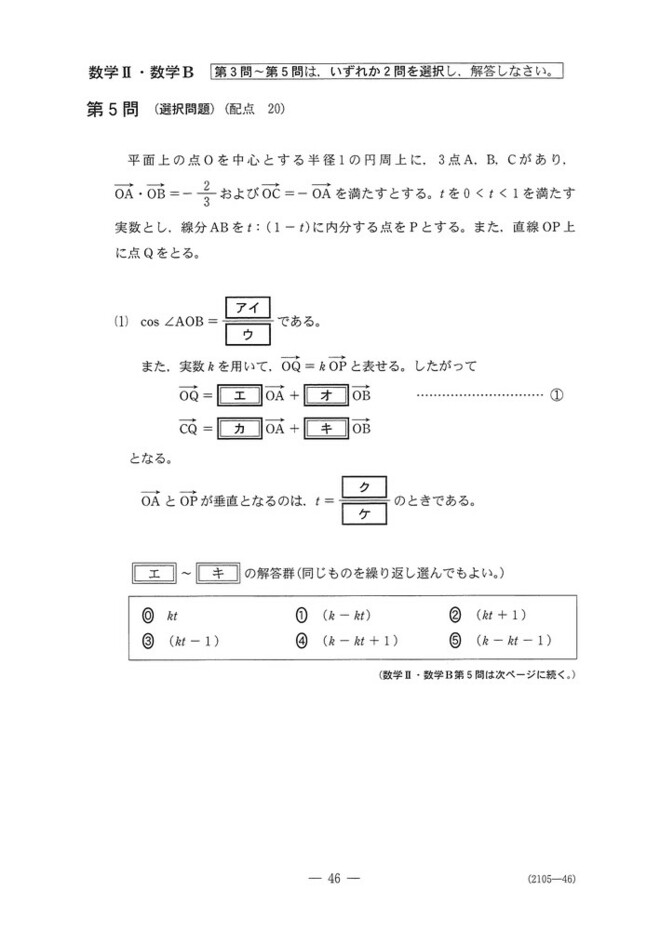
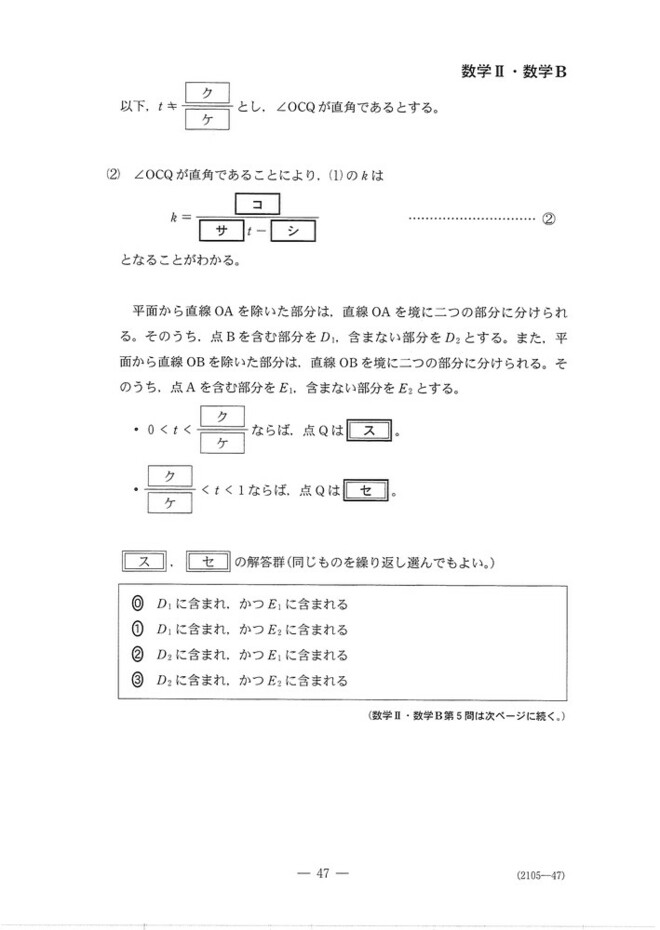
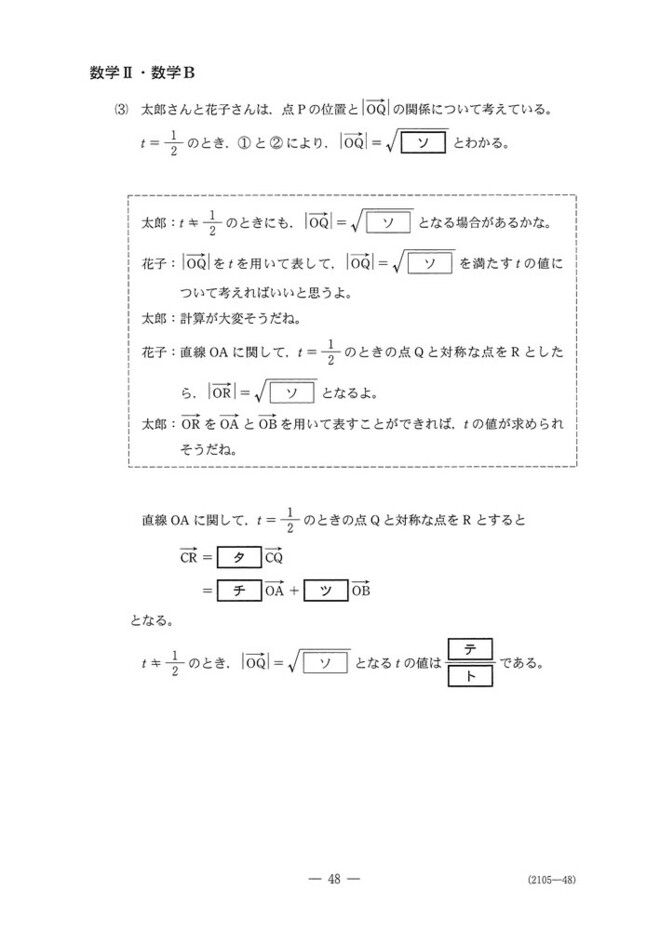
ベクトルの問題です。
(1)ア~ウ:OA=OB=1なので、内積の値がcosの値そのものですね。
エ~キ:OP=(1-t)OA+tOBを使って計算していきます。
クケ:OAとOPの内積が0になるtを計算します。
(2)コ~シ:これまたCOとCQが内積=0になる条件を考えます。
スセ:kの符号から、Qがどこにいるかが分かります。
(3)ソ:kの値を②から計算すれば、①からOQが求まります。
タ~ツ:CR=-CQが分かってしまえば計算できます。
テ、ト:正直、問題文の誘導がうまく理解できなかったので、太郎君が「計算が大変そう」と言っていた方法でごり押しで解きました。正直、太郎君には悪いですが、大して大変じゃなかったです笑。
OQの式をtで表現して、|OQ|=√ソになるtを2次方程式を解いて調べます。
<筆者の回答>

