このシリーズでは、平成の九大理系数学の後期入試の問題を1年ずつ遡って解いていきます。
25回目の今回は1995年になります。
第1問

球の接線群に関する問題です。
(1) AとEの位置関係を考察してあげましょう。
Eの中心Cを通って、法線ベクトルがOAとなる平面がHとなります。O,C,Aが同一直線上にあるので、実質OCの長さが求まれば事足ります。
(2)V1については積分計算で、V2についてはEの半径と高さCAが分かれば求まります。
<筆者の解答>

第2問

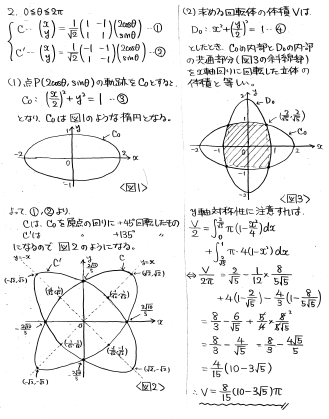
楕円の回転に関する問題です。
(1)点(2cosθ, sinθ)の軌跡C0は楕円となり、CはC0を原点の周りに45°回転、C'はC0を原点の周りに135°回転した図形になります。
(2) C, C'のまま考えるのは難しいので、元のC0に戻してあげましょう。C0を90°回転した楕円をD0とすると、C0とD0の共通部分をx軸周りに回転させれば、体積を求める立体になります。
<筆者の解答>
第3問

絶対値を含んだ積分の関数を考察する問題です。
(1)aの値によってx+aの符号が変わるため、場合分けして計算します。
(2) 最大値を取りうるのは真ん中の領域のみなので、そこで微分してあげましょう。
<筆者の解答>

第4問

容器に残る水量に関する問題です。
原典の図が見つからなかったので、長さ1の辺を勝手に回転軸PQとさせて頂きました。
他のどの辺を回転軸にしても本質的な解き方は変わりませんので、一番対称性がよく楽なPQ=1の辺としました。
(1)回転軸に垂直な方向に容器を見れば、そこでの水の面積がそのまま体積となります。tanθの値によって形状が変わるので、場合分けしましょう。
(2) (1)の結果を素直にtで微分してfをtanωtの関数として表現してあげます。単調性から微分するまでもなく最大値が分かってしまいます。
<筆者の解答>
