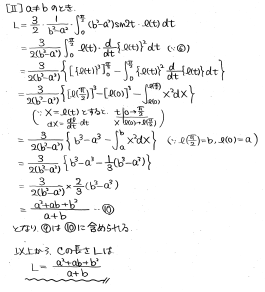このシリーズでは、東京医科歯科大学の数学の問題を解いていきます。
20回目の今回は2003年です。
第1問

複素数に関する問題です。
(1) aとbの条件から|z|=0か|z|=1しかありえません。前者はz=0しかなくbを自動的に満たすので、後者をz=cosθ+isinθとして、z+z*=2cosθが整数になるようにθを決めていきます。
(2) dはそのままだと分かりにくいので、対偶を取って「z^2-pz+q=0ならば|z|≦1」と言い換えてしまいましょう。つまり「2次方程式z^2-pz+q=0の解の絶対値は全部1以下」ということです。
こうなれば、この2次方程式が実数解を持つのか虚数解を持つのかで場合分けが発生することが分かります。
前者の場合はおなじみの「軸の位置」「端点の符号」で調べていくわけですが、後者の場合はp=z+z*, q=zz*となるので実は(1)でそうなるzを調査済みです。
<筆者の解答>


第2問

1次変換に関する問題です。
(1)これは背理法で証明するとよいです。Pk=Pk-1となるkが存在すると仮定すると、Pk=Pk-1=・・・=P1=P0となって、P1≠P0と矛盾することを言います。
(2)P0→P1, P1→P2の2つの条件から行列Mを構築することを考えます。sinθ=0となる時が例外扱いとなるのですが、それ以外の時はMが「原点の周りにθ回転する1次変換」となることが示せます。
(3)A~Fを図示すると、単位円周を6等分する点になります。これと(a)を見ると「Mは回転行列に違いない」と即断即決しそうですが、そうとは限らないことに注意です。
Mを成分で置くと、P1=Bの条件からMの左半分の成分は確定できます。
(a)を満たすなら、少なくともP2はA~Fのどれかになっているはずなので、それによって場合分けをするとよいでしょう。(1)と(2)の知見を活かしつつ(c)を満たすものだけを抽出していきます。最後に忘れがちですがMが逆行列を持つことにも注意です。
<筆者の解答>



第3問

曲線の長さを計算していく問題です。
(1) Cの接線の式を調べることでQ,Rの座標を求めてしまえばよいでしょう。
(2)ただ微分するだけの問題ですが、この結果が実は(3)に生きてきます。
(3) Cの長さLを公式に従って計算していくと、積分の中身がsin2t×l(t)の形になって、そのままだと詰まってしまいます。
ここで、(2)の結果からsin2tがl(t)の微分の式で書き替えられることに気付くと、部分積分が使えるんじゃないかと発想できるわけです。
この変換ができるのがa≠bのときなので、a=bの時を例外扱いとして計算していきましょう。部分積分をした後はX=l(t)と置換すると見通しよく計算できます。
<筆者の解答>