このシリーズでは、京都府立医科大学の数学の問題を解いていきます。
20回目の今回は2003年です。
(手書きでの問題文を提供して下さったせがわさん、ありがとうございます!)
第1問

整数問題です。
yn=xn-(-1)^n×x0とおいて、ynが3で割り切れることを数学的帰納法で証明していきます。その際、yk+1をできる限りykの式で表現することがポイントです。
<筆者の解答>

第2問

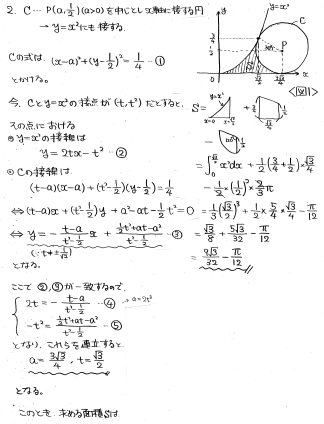
放物線と円が接する条件を考える問題です。
円と放物線が(t,t^2)で接するとすると、x=tでの接線の式が2つとも同じになります。それを利用することでaとtが求められ、図に描けば積分も交えて面積が計算できます。
<筆者の解答>
第3問

確率の問題です。
(1)~(4)
Aがa,b,cの3つのカードを引いたときに、Bがどのカードを引けばいいのかを考えます。
(5)~(7)
1を引く確率をpとして、このpを使って計算していけばよいです。
<筆者の解答>

第4問

球の配置に関する問題です。
(1)Tがα,β,xy平面に接してSに内接する条件からTの中心座標と半径を調べていきます。内接する条件は、中心間距離=半径の差、で考えることができます。
(2) (1)ができていれば瞬殺です。
それにしても、この年のセットは、京府医にしては全体的にあまりに簡単じゃないでしょうかね?
<筆者の解答>
