今日行われた2023年度共通テストの問題を見ていきます。
次に数学ⅡBを扱います。
※試験当日に解いており、ミスがあるかもしれません。
<略解>

※採点の結果、第3問のスセソ、第5問のコ、シにミスがありました。
正しくはスセソが180,コが0, シが2となります。申し訳ありません。
<個別解説>
第1問[1]


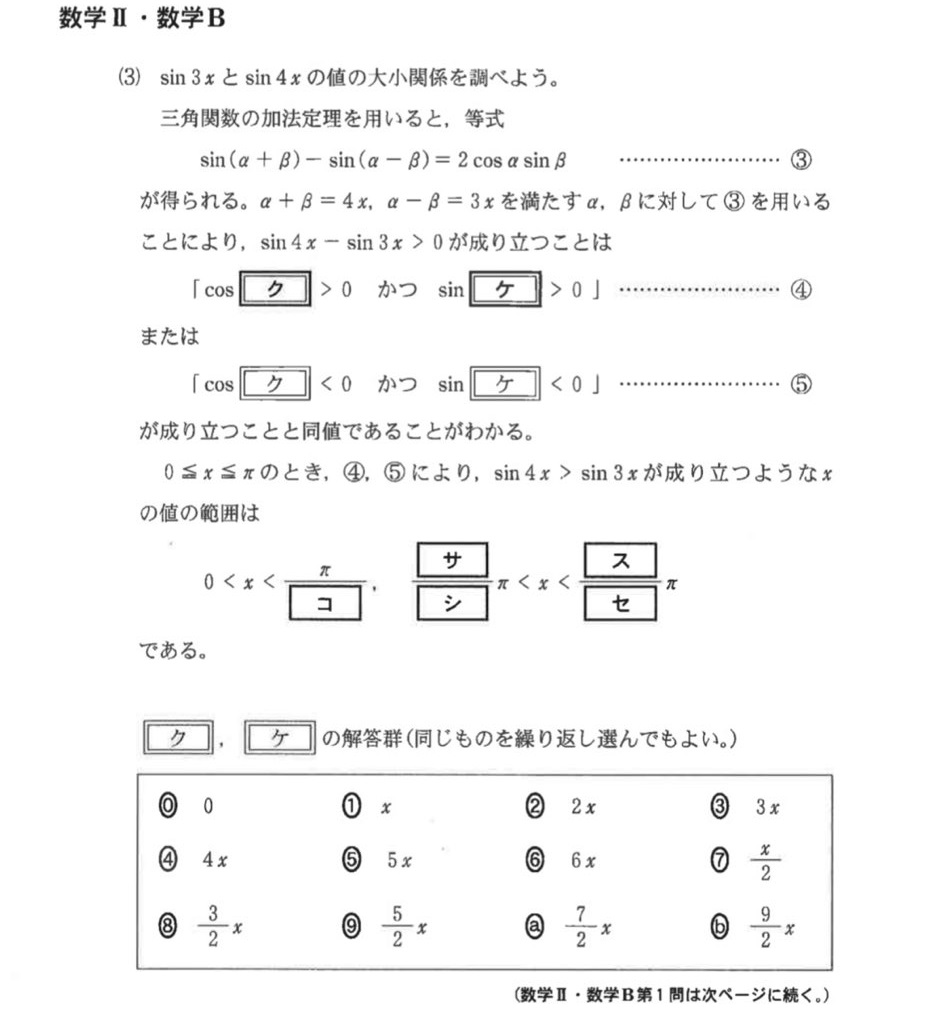

三角関数の不等式に関する問題です。
(1)
ア、イ:具体的にxに値を代入して計算すればよいです。自信がなければ単位円を描きましょう。
(2)
ウ、エ:2倍角の公式を使えばよいですね。
オ~キ:三角関数の不等式が出てきたら、基本的には単位円を使って視覚的に解くのが鉄板です。
(3)
ク、ケ:和積の公式が予め用意されているので、α+β=4x, α-β=3xとして代入してしまいましょう。
コ~セ:0≦x≦πの範囲では必ずsin(x/2)>0となるので、⑤は考えなくてもよくなります。この範囲に注意して、cosの不等式を解きましょう。
(4)sin3x>sin4xとsin4x>sin2xを個別に考えて、あとで合体させます。
前半の方は、(3)の結果の「逆」を考えてあげればよく、後半の方は、(2)でxを2xに変えたものに等しくなっています。
<筆者の回答>

第1問[2]


対数に関する問題です。
(1)ツ:対数の定義そのものですね。
(2)テ~ナ:真数を指数の形に直して考えてあげればよいでしょう。トナについては、底を3に変換すると見通しが良くなります。
ニ:対数の定義に従って直していくだけですね。方や2の累乗で片や3の累乗で両立しえないので矛盾、という論法ですね。
ヌ:同じように考えれば、a^p = b^qとできます。aとbの偶奇が違っていれば、方や偶数で片や奇数となって、絶対に両立しえないですね。
<筆者の回答>

第2問[1]


3次関数の増減を考える問題です。
(1)
ア:f(x)=0を解けばよいでしょう。
イ~ク:これも展開して微分するだけの基本問題です。この式からどこで極値を取るかが分かるので、極値も計算可能です。極小値と極大値を逆にしないように注意です。
(2)円柱の高さは相似を使ってxの式で書けるため、Vはf(x)の類似系の3次関数で書けます。もっといえば、(1)でk=サとした場合に該当します。
今回の範囲では、極大値=最大値となります。
訂正:答案では係数の5π/3をかけ忘れてました・・・正解は180です。
<筆者の回答>

第2問[2]




積分とその応用問題です。
(1)どちらも定義通りに計算していくのみです。
(2)
ノ:S(t)の式を具体的に計算して、それが400以上となるようなtを探します。2次不等式を解くよりも、直接値を代入して目途をつけた方が速い気がします。
ハ:関数が単調増加で積分区間の長さが一緒なので、積分=面積は、40~50の方が大きくなります。
ヒ:ハを利用して、0~40の積分値と0~50の積分値が、400を超えるか否かを調べていきます。
<筆者の回答>

第3問
統計の問題ですが、この大問を選択する受験生は殆どいないと思われ、解いている時間もなかったので、今回は省略させていただきます。
第4問





預金を題材にした数列の問題です。
(1)
ア~オ:預金×(1+利息)+pで翌年の預金が求まる、という漸化式を立てればよく、特性方程式を利用することで等比数列の形にできます。
カ~ケ:指数の番号については、迷ったらn=1とかn=2など具体的な小さな値を入れて妥当性を確認すればよいです。ケは典型的な等比数列の和になります。
方針1,2どちらの方法をとってもanの一般項は同じ式になります。
(2)
コ~セ:10年目の終わりにpを足したものがa11になりますので、そこから不等式が立ち、あとはpについて解けばよいだけです。
(3) anの10の部分が13に変わるだけで、pに関わるところはanと全く一緒ですね。
<筆者の回答>

第5問




三角錐に関するベクトルの問題です。
(2)で具体的な辺の長さと角度が出て来ますが、あくまでこれらは(2)限定の設定であることに注意が必要です。(3)以降は再び一般の場合に戻るので混乱しちゃいそうです。。
(1)
ア~エ:中点なのでベクトルの平均を取るだけで楽勝です。
オ:これも内積の定義から明らかですね。
(2)
カ:オに具体的な値を代入すればお終いです。
キ:PAとPDの内積が0になるという式を、Aを始点にしてすべて書き直してしまうとよいでしょう。
(3)
ク:こちらもPA・PQ=0をA始点で変形すればOKです。内積をcosを使った式に書き直せばよいでしょう。
コ:与式を同様にcosを使った式に書き直していきますが、選択肢にcosθが入ってませんね。ここはθ=45°を引きずってると考えて、一番妥当そうなものを選ぶと3ですね。
右辺にもcosθが出てくることを失念してしまいましたね。正解は0です。
サ:ABcosθ=AB', ACcosθ=AC'となることに気付けたかがポイントになります。これを利用することでAB', AC'の各ベクトルがAPベクトルの定数倍で書けるので、APをどう内分するかを調べられます。
シ:k=1ならB'=C'となり、これはAB=ACと言い換えられます。これで「2辺が等しく、それに挟まれる角が等しい」という合同条件がバッチリ満たされます。
訂正:これだけでは不十分で、追加でB', C'がAPの中点になるので、△APBと△APCはそれぞれB,Cを頂角とする2等辺三角形ですね。ということで、満額回答は2です。
<筆者の回答>
