旧帝大の文系向けの過去問を取り上げます。理系との共通問題は理系の記事を参照して頂くこととし、基本は文系ユニークの問題のみ取り上げます。
この記事では東京大学の1995年の問題を取り上げます。
理系の記事はこちら↓
平成の東大理系数学 -1995年- - ちょぴん先生の数学部屋 (hatenablog.com)
第1問

理系第1問との共通問題です。詳しくは理系の記事をご覧ください。
第2問

8角形の面積に関する問題です。
(1) PnPn+1ベクトルを定義に従って次々に足していき、P0P8ベクトルが0になることを示しましょう。
(2)図を描けば、8角形は正方形から直角二等辺三角形を4隅から切り取ったような図形になります。
(3)P0P4の長さは三平方の定理で求まるので、面積の条件と連立すればOKです。
<筆者の回答>

第3問

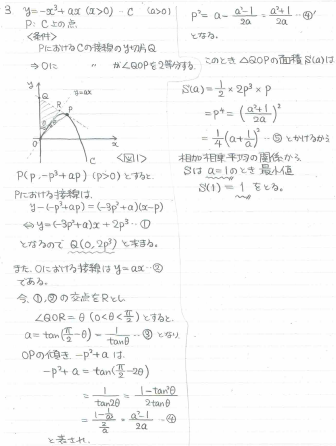
接線と角の2等分線に関する問題です。
aを固定したときのPの座標を、tanの加法定理を使って計算していくとよいでしょう。
<筆者の回答>
第4問

球形の容器の体積に関する問題です。
水面の面積を積分すると、θ傾けたときの容量が計算できるので、水の投入速度と満杯になる条件を使って、θを求めていきましょう。sinθの3次方程式に帰着します。
<筆者の回答>
