このシリーズでは、平成の東大理系数学の問題を1年ずつ遡って解いていきます。
東大の数学の問題は、難易度は高いですが良問の宝庫であり、演習価値が非常に高いです。
(時々、どうしようもなく難易度が高く、筆者の力量でも解けない問題が出てくることがありますが、どうかご容赦くださいm(_ _)m )
13回目の今回は、2007年の問題です。
第1問

多項式の係数の性質を調べる問題です。第1問にしては取っつきにくさが際立つ問題でしょう。
kが小さいところで、まず考えてみましょう。今後説明のために、Pk(x)=(1+x)^k×P(x)と書くことにします。
k=1のとき、
P(x)=a0+a1*x+a2*x^2+・・・+an*x^n、
P1(x)=b0+b1*x+b2*x^2+・・・+bn*x^n+bn+1*x^(n+1) とおいてみます。
この問題では、n次以下の項にしか興味がないので、P(x)はn次式とすれば十分です。
この両者をつかって、aとbの関係式を求めてみると、係数が1しか登場しない足し算引き算でかけるので、bが整数ならばaは整数になりますね。
これでk=1のケースの証明が終わりました。
さて、kが2以上の場合はどうするか?
よくよく考えてみると、Pk(x)=(1+x)^k×P(x)=(1+x)×Pk-1(x)となるので、k=1のケースに実質的に持ち込むことできます。
つまり、Pk(x)のn次以下の係数が整数 → Pk-1(x)のn次以下の係数も整数 が言えるわけです。
これをk回繰り返すことで、P(x)のn次以下の係数も整数 も言えることになります。
やや特殊な証明の仕方ですが、これで何とか解けました。。。
<筆者の解答>

第2問

条件を満たす辺の長さの総和を求める問題です。
条件1,2を総合すると、△OPk-1Pkは全部相似で、長さは1+1/n倍ずつ増えていくことが分かります。
よって、akは等比数列となり、初項も余弦定理で簡単に計算できるので、akの一般項、級数snが次々に計算できていきます。
snの極限は、(1+1/n)^nの入っている部分と、cosの入っている部分とに分かれるので、それぞれを考えます。
前者は、ネイピア数eの定義そのものです。後者は、変形することで、sinx/x→1 (x→0)の形に持ち込みましょう。
ちなみに、この問題は、対数螺旋という曲線の長さを折れ線に分割することで考えている問題で、この曲線は、極座標でr=e^(θ/π) (0<θ<π)と書くことができます。
この対数螺旋の式を曲線の長さの公式に代入して積分計算しても、全く同じ答えが出てきます。
<筆者の解答>

(参考:対数螺旋の長さ)

第3問

放物線上の2点をつないだ線分を一定の比に内分する点の存在範囲を考える問題で、条件処理の煩雑さが厄介な難問です。
(1)まずは常套手段、PとQのx座標をα、βと文字で置いてしまい、Rの座標(a,b)をα、βで表現します。
ここからα、βを消したいのですが、方や1次式、方や2次式となっていて、かつ非対称な式になっているので、残念ながらうまく消えてくれません。。
なので、泣く泣く、片方だけを消して条件処理することにします。
まずβを消去してみましょう。するとαの2次方程式が出来上がり、αは-1と1の間にいないといけないので、この方程式が-1と1の間に解を持つa,bの条件を調べることになります。
ここまででは、βの範囲を全く考慮できていないので、今度はαを消去して、全く同じ議論をβについても行います。
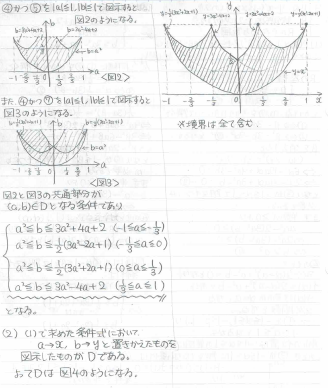
この2つの議論を合体させたものが、求める条件です。この合体が非常に面倒なのですが。。。グラフに書いてしまうのが直観的で間違いがないでしょう。
(2)は(1)で求めた条件を図示すればOKです。
<筆者の解答>

第4問

行列の掛け算の計算問題です。誘導通りに計算をするだけの易しい問題です。
(1)は条件が色々出てきますが、総動員すれば簡単に証明できます。
(2)は、(1)からP+Qが単位行列だと分かります。これでP,Qの片方を消すことができるので、連立方程式の要領で求めることができます。
不安でしたら、出てきたP,Qが(1)の条件を全部満たすかをチェックしてみてください。
(3)は、(1)(2)をつかって、Ak=kP+(k+1)Qと書くことができます。訊かれている行列の積ですが、最初の数個で実験すると答えが予想できるので、それを帰納法で証明すればよいでしょう。
<筆者の解答>

第5問

裏が出た瞬間努力が無に帰す、いわば「賽の河原」のようなシチュエーションを題材にした確率の問題です。
最終的にm個ブロックが積みあがるためには、最後のm回全てで表を出さないといけません。最後のm回の直前が裏になる(それより前の経緯は関係ない)のですが、
ここで、m=nの場合だけ例外であることに気が付きますでしょうか?m=nのときは、表が出続けるm回の「直前の一回」がない、つまり裏が出るスキがないのです。
この問題では、終始m=nのケースだけ例外扱いで話が進みます。
(1)は上記の通り、(2)は(1)の確率のΣです。
(3)は、「第1セットがm段かつ第2セットがm段以下」+「第1セットがm段以下かつ第2セットがm段」- 「第1セットと第2セットが両方m段」 で求まります。
<筆者の解答>

第6問

不等式評価の問題で、こちらは発想面で難問となっています。
(1)は、積分を計算して微分で・・でも行けるとは思いますが、面積の大小で考えてしまうのが、一番楽でしょう。
なぜそう考えるかというと、中辺が積分というまさに面積を表した量になっていて、右辺の式が、なんとなく台形の面積っぽく見えるからです。
左辺が少し思いつきにくいですが、接線を考えることで解決します。
さて、(2)については、「(1)を使って」とあるので、中辺の積分を計算してlogが出てくるから、logの中身を2にすれば瞬殺!!と思いきや、実際にやってみると、
0.66<log2<0.75となってしまい、問題文の式より評価が甘くなってしまいます。困りましたね。。。「(1)を使って」とある問題は、ただ使うだけでは解けないんですよ。
ここで、ヒラメキが必要になるのですが、2の代わりに2^pというより一般的な数を代入してみましょう。これでもlog2が出てくることに変わりはありませんので、
すると、log2がpの式ではさめることになります。左辺の方はpが大きくなると小さくなっていき、逆に右辺の方はpが大きくなると大きくなっていきます。
もっと厳しく評価したいということは、両者の幅を狭める必要があります。ということはpをどんどん小さくしていけばよいことになります。
ではpに何を入れればよいか?1はダメだったので1より小さい数にしないといけません。式に2^pが登場しているので、これを比較的馴染みのある数に計算しやすいpを持っていきたい・・・と考えると、p=1/2はどうだろう?と発想できるわけです。こうしれば√2という比較的馴染みのある数を登場させることができます。
p=1/2としてみると、
12-8√2 < log2 <1/√2 となります。あとは√2の式をうまいこと近似できれば行けるかもしれません(あくまでかもしれない、です。これでもダメな可能性もまだあります)。
お目当ての数値を出そうとすると、√2の値も1.414 < √2 < 1.415 という小数点以下3桁の精度まで使わないとたどり着けません。このあたりも試行錯誤が必要になっていきます。
ここまでして、ようやく0.68< log2 <0.71にたどり着きます。
この問題を通じてわかることは、いかに近似値を精度良く出していくのが大変か、ということですね。
<筆者の解答>
