2022年も大学入試のシーズンがやってきました。
今回は、東京大学の理系数学に挑戦します。
<概略> (カッコ内は解くのにかかった時間)
1. 積分を含んだ関数の増減 (15分)
2. 数列の最大公約数 (20分) ※(3)自信なし→[3/1 きちんと解けました]
3. 点の距離に絡んだ面積の増減 (40分)
4. 直線の存在証明 (35分)
5. 立体の体積 (30分)
6. ベクトルの絡んだ確率 (60分) ※(2)は解けてません→[3/3 (1)含めてなんとか解けました]
計200分
<体感難易度>
1<5<3<4<2<<6
一昨年並みの難易度に難化したと思います。2017年以来5年ぶりに確率の問題が復活しましたが、捨て問レベルの超難問です。
他の問題にしてもなかなか手ごたえがあります。
<個別解説>
第1問

積分を含んだ関数の増減に関する問題です。今回のセットの中では最も易しい問題ではありますが、決して簡単ではありません。
(1) f'(x)の方が先に綺麗に求まるので、符号を調べましょう。きちんと最小値を与えるxの値が求まります。
(2) (1)の結果を使って実際にf(x)の積分を計算します。logを含んだ積分なので、勿論部分積分を使います。計算を進めると∫dt/costの形の積分が登場しますが、これはX=sintと変換して部分分数分解を使う典型問題です。
<筆者の回答>

第2問

数列の最大公約数に関する問題です。おそらく、「フェルマー数」という概念が背景にあるものと思われます。筆者は(2)までは自信をもって解答できていますが、(3)は自信がありません。。。
(1)漸化式を使って、帰納法で証明するとよいでしょう。
(2)kを一旦固定した状態で、ak+1以降をakで割った余りを考えると、a1,a2,・・・が順番に出てきます。ここから、nがkの倍数であればanはakで割り切れることが分かります。
[3/1追記]議論が曖昧な答案になっていたので、十分性だけでなく必要性のチェックも加筆しました。
(3) (2)の結果を使うと、a2022はa2とa3とa337で割り切れ、a8091はa3,a31,a29で割り切れることが分かり、公約数がa3の倍数だとは分かるのですが、それが「最大」公約数なのかの確証がとれませんでした・・・
[3/1追記] きちんと解くことが出来ましたので、解説します。
(2)の検討結果を使うと、8091=2022×4 + 3なので、a8091はa2022で割るとa3=5余ります。よって(a8091)^2をa2022で割ると25余ります。ユークリッドの互除法から、求める最大公約数が、a2022と25の最大公約数(=25の約数)に等しいことが分かります。
a2022は、2022が3の倍数なので5で割り切れますが、実はanは25で割り切れないことが帰納的に分かるので、最大公約数は5で確定します。
<筆者の回答>


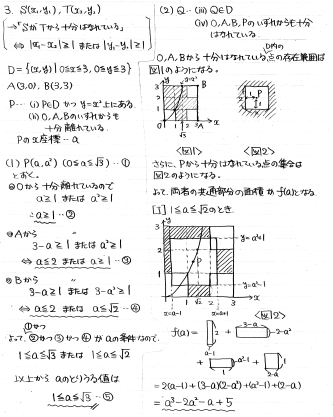
第3問

点の距離に絡んだ面積の増減に関する問題です。
「十分に離れている」という用語をうまく図形的に翻訳して進められたかがポイントです。
(1) PがO,A,Bから十分離れている条件を順に処理していきます。代数的に処理してもいいですが、O,A,Bから十分に離れていて第1象限に入っている点の集合は、実はDからO,A,Bの周りにある1×1の正方形をくり抜いたものになります。これを利用すると、図形的にaの条件はすぐに分かってしまいます。
(2) Pから十分に離れている領域はPの四方に広がる2×2の正方形の外側になります。これと上記の領域の共通部分の面積を考えていきます。2×2の正方形がDにすっぽり入るかはみ出すかで場合分けが生じます。
(3) (2)の結果の増減を調べればOKです。
[3/12追記] 最後の部分で計算ミスをしていたので、修正しました。
<筆者の回答>

第4問

直線の存在証明に関する問題です。
(1) Pを(a,b)と一旦固定し、lの式をy=m(x-a)+bと定めます。Cとlを連立した方程式が3つ実数解を持つようなmが、(a,b)がどんな値でも見つけて来れることを説明しましょう。
3つ実数解が3つ出てくるようにmの条件を決めていくと、最終的に(mの3次式)>(mの2次式)となります。mを十分大きくとれば必ず3次式が勝つので、mが必ず存在することになります。
(2) (1)にさらに面積の情報を付け足します。3次関数と直線がx=α,β,γ (α<β<γ)で交わってるときにα~βの面積とβ~γの面積が等しいなら、(x-α)(x-β)(x-γ)をα~γで積分した結果が0になります。この性質を使うと見通しがよくなり、あとは解と係数の関係を使ってあげればよいでしょう。
<筆者の回答>


第5問

立体の体積を計算する問題です。
一旦Pを線分AB上に固定して、その時のMの動く範囲を考えるとよいでしょう。すると、Mを通る面でKを切断すれば、断面積が求まり、それを積分すればKの体積が求まります。
<筆者の回答>

第6問

ベクトルの絡んだ確率に関する問題で、久々に復活した確率の問題です。でも、よりにもよってこんな超難易度の問題にしなくても・・・個人的に本セット最難問であり、(2)は解かずに捨ててしまいました。。
表になった時におまけについてくるvkが曲者で、kが「今まで累計で出た裏の回数」というややこしい設定になっているせいで、難易度が跳ね上がってます。
vkを詳細に見ていくと、実は3つのベクトルしかありません。この3種類のベクトルをa,b,cとすると、OXにaとbとcが同じ数だけ足されるとa+b+c=0となってXはOに戻ってきます。XがOに戻る方法は逆にこの方法以外ありません。
まずもってこの知見に気付けないと、この大問は全く覚束ないです。
(1) N=8でも結構大変な問題です。
a,b,cが8回の中で一度も足されない、一度ずつ足される、2度足されるの3パターンで場合分けして表裏の出方を虱潰しに調べていくほかありません。それもこれも全部kの設定のせいです(怒)
この(1)を解き終わった時点で力尽き、(2)は解くことを放棄しました。
[3/3追記] 出方の調査で数え漏れがあったので、修正しました。
(2) (1)ですら大変だったのにN=200とかふざけてるんですかね?実はもっとうまい方法があるのかもしれませんが、私には思いつきませんでした。後日改めて考え直してみることにします。
[3/3追記] 駿台さんの解答速報をチラ見してヒントを得た状態で、なんとか最後まで解き切れました。
X200=Oとなるには、rが3の倍数でないといけないことは(1)での考察から分かっていますので、Prはrが3の倍数になるときに限って調べればOKです(rが3で割り切れなければPr=0です)。ここまでは、初見で諦めずに書けましたね・・・後悔後悔。
その後の発想が、解答速報を見ないと思いつかなかった部分で、
「k回目の裏とk+1回目の裏の間に出てくる表の回数をAkとして、Akの合計をa,b,cの各ベクトルごとに考察する」
です。
これは初見では全く思い浮かびませんでしたね・・・(そもそも(2)を解く気力が残ってなかったのが正直なところですが)
このようなAkの組み合わせの個数は、「ボールn個、仕切りm個を並び替える方法の総数」の考え方で求めることができます。
Prの最大値については、前後の項との比を取って1との大小関係を調べる、というお馴染みの方法で求まります。
<筆者の回答>

