このシリーズでは、平成の東大理系数学の問題を1年ずつ遡って解いていきます。
東大の数学の問題は、難易度は高いですが良問の宝庫であり、演習価値が非常に高いです。
(時々、どうしようもなく難易度が高く、筆者の力量でも解けない問題が出てくることがありますが、どうかご容赦くださいm(_ _)m )
2回目の今回は、2018年の問題です。
第1問
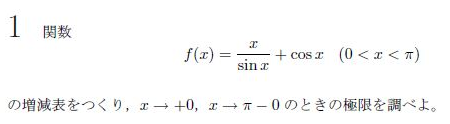
関数の増減と極限を求める問題です。非常に易しい問題ですので、完答必須です。
普通に微分を計算して、符号を調べればよいのですが、分子の計算に一工夫必要です。
分子はすべての項にsinかcosが入っているので、どちらかで括りたいところです。xcosxがこれ以上イジれない形になっているので、cosxで括ればいいという発想に至ります。
<筆者の解答>

第2問

二項係数に絡んだ整数問題です。難易度としては、合否を分ける程度の差がつく問題といったところです。
(1)は、二項係数を階乗の形で書いてバッサバッサと約分していきます。すると、分母にn(n+1)が残りますが、これが偶数なので2で割り切れる、ということを見落としがちなので要注意です。
あとは、分子の2n+1と、分母のn(n+1)/2が互いに素なことを説明すればお終いです。
(2)は、(1)で作ったanの漸化式を利用します。2通りの解き方があるので、それぞれ紹介します。
(解法1) q/pが(1次式)/(2次式)の形をしているので、nが十分大きいところでは q/p<1になります。よって、anは途中から単調減少になるわけです。
ここで、anがどこかの瞬間で1未満になってしまえば、そこから先は全部1未満になるので整数になりません。よって、anが1以上になっているnについて全部調べて、整数になっているものを列挙すればよい。 というのが解法1です。
(解法2)anが、(qnの掛け算)/(pnの掛け算)×a1の形になることに注目します。
(1)で求めたように、qn= 2n+1なので、qnは奇数、ということはqnの掛け算は奇数になります。一方、pnは、p3=6となるから、そこから先ではpnの掛け算は偶数になります。よって、(qnの掛け算)/(pnの掛け算)は、約分しても分母に2が必ず残ってしまうので整数になれないわけです。そしてa1も奇数なので、分母の2はどうあがいても消せません。 このようにして解くのが解法2です。
<筆者の解答>


第3問

点の存在範囲を調べて、その面積を求める問題です。やや難しめの問題だと思います。
まず、問題文にあるベクトル表記が分かりにくく、PとQの2つが動くので捉えづらくなっています。こういう時は、どちらかを固定して考えると見通しが良いです。この場合はQを先に固定して考えるとスッキリします。
結論としては、放物線をx軸方向にスライドさせたときの通過範囲が、考える領域になります。
さて、次に第2の関門が待ち構えています。kの値によって、領域の形が変わってしまうのですよ。直観的には、「放物線があまりスライドしない場合」と「放物線がスライドしすぎる場合」の2通りです。この場合分けの存在に気づけるかが、この問題のキーポイントです。
この場合分けに従って面積を計算しましょう。
<筆者の解答>

第4問

3次方程式の解の配置に関する問題です。この問題は易しめなので、ぜひ押さえたいです。
とにもかくにも、f(x)のグラフを描くのが第1歩です。その形状から、条件1については簡単に処理できるでしょう。
次に、βの配置についてですが、グラフから、βは-aからaに収まっています。よって、β>1となるには、aの左に1があればよいわけです。
<筆者の解答>

第5問

複素数平面の問題です。計算処理に発想が要る難問です。
(1)は、まずuについて計算するのですが、一旦xy平面の世界で考え、かつ相似やベクトルなど図形の知識を使っていくと計算量を減らすことができます。そのうえで、最後にzを使った複素数平面の世界に戻してあげればよいです。
次にw*/wについてですが、z*が邪魔なので、これをなんとかして消したいというモチベーションでにらめっこすると閃くかもしれません。
最終的に|w+w*-1|/|w|は定数になります。
(2)は、(1)を使わずとも解くことが可能ですが、|w+w*-1|/|w|を使うとショートカットができます。いずれにせよ、複素数のままでは考えにくいので、やはりw=x+iyとおいてxy平面の世界に落とし込んで考えていきましょう。
<筆者の解答>

第6問

くねくねした水道管のような立体の体積を求める問題です。質・量ともに非常にボリュームが多い難問で、本番で最後まで解き切れた受験生はほぼ0だったと思われます。
(1)は円柱+半球2つを軸方向に切断したときの断面を、2個分考えることになります。
(2)は、V1とV3の共通部分が、V2にすっぽり覆われる条件を考えることになります。(1)で描いた断面図が、V2の断面=半径rの円の内側に入る条件と言い換えてもいいです。
V2の断面中心から、最も遠い点について考察するのが鍵です。
(3)は、(4)を解くための寄り道で、3つの集合の和を考える問題です。ここで、(2)から、「V1とV2とV3の共通部分」=「V1とV3の共通部分」に気が付けるかがポイントです。
(4)は、S,Tを計算して、(3)を使ってVを計算するという流れです。
Sは簡単に計算できるのですが、問題はTの計算。
今までy=tで切った断面を考えてきましたが、これだと計算が大変になってしまいます。ここで、気持ちを切り替えてz=uで切った断面を考えると、スッキリ計算できます。
<筆者の解答>

