このシリーズでは、平成の東北大理系数学の後期入試の問題を1年ずつ遡って解いていきます。
2回目の今回は2018年になります。
第1問

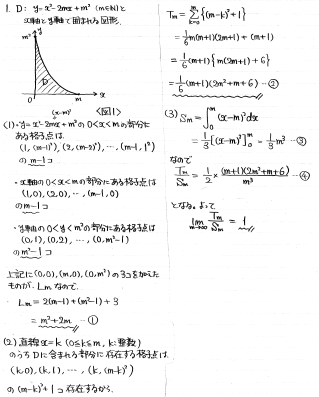
格子点の個数に関する極限の問題です。
放物線の式がy=(m-x)^2と直るので、xが整数ならyも必ず整数になります。
(1) 放物線上の格子点と、軸上の格子点を数え上げて足せばよいですが、ダブルカウントに注意しましょう。
(2) 直線x=k (k=0,1,・・,m)上にある格子点を数えて足し上げます。
(3) Smは積分で容易に求まるので、極限計算も容易です。
結果は1となりますが、これは「mが十分大きければ、Dの面積はおよそDに含まれる格子点の個数で見積もれる」ことを意味しています。
<筆者の解答>
第2問

円周上の三角形の面積に関する問題です。
(1) 図形的に証明します。α+βがπよりも大きいか小さいかで場合分けが起きますが、結局同じ式になります。
(2) (1)の結果を使って、考える面積を∠AOXの式で表現してあげればよいです。
<筆者の解答>

第3問

確率の問題です。(3)に極端に比重が寄っている問題と言えます。
(1) 2回で全てが黒になるには、同じ数が2回出ればよいです。
(2) 3回で全てが白になるには、横に1列ずつ白に切り替わるか、縦に1行ずつ白に切り替わるかの2択です。
(3) これがメインディッシュです。
最初が黒なので、奇数回裏返れば「白」に、偶数回裏返れば「黒」になります。
これを基に各板が、サイコロがどう出れば裏返るかを調べ、各目の出る回数の配分を調べていきましょう。
<筆者の解答>


第4問

数列の極限に関する問題です。
(1) 漸化式から、a2m-1の漸化式を作ってあげればよいでしょう。この漸化式を作った時点で、実は漸化式の中にある絶対値は外しても構わないと分かります。
(2) (1)の結果を使ってa2mの一般項を求めればOKです。
(3) a2m-1, a2m, いずれもm→∞で同じ値に収束します。
<筆者の解答>

第5問

正四面体に関する図形問題です。
(1)一見して、Gが正四面体ABCDの中心だと分かりますので、ベクトルというよりかは、中学数学の要領で図形的に解いてしまった方が早いでしょう。
(2) Gを原点にするxyz座標を設定すると見通しがよくなります。このときにP(zx,y,z)とおくと、Lは球対称な式になります。
<筆者の解答>


第6問

積分に関する極限の問題です。
(1) anをs=2logxと置換すると、e^s*s^nの0~1での積分に置き換わります。示す不等式を見るとn+1が分母にあるので、s^nの部分だけ積分すれば良さそうだと想像できますね。なので、e^sの部分を定数で置き換えてしまいましょう。
(2) anを一回部分積分して、anとan-1の関係式を求めましょう。
(3) (2)でpnとqnの両方の漸化式が求まっていますが、pnを直接計算しようとすると極限が(少なくとも高校数学の範囲では)うまく計算できません。
(※具体的にはΣ(-1)^n/n! の極限が必要になり、それを計算するには大学数学の「テイラー展開」の知識が必要です)
(1)で求まった不等式ではさみうちを使えばan→0 (n→∞)が分かるので、qnの方を検討すると、実は解くことができます。
qnの漸化式の処理は、両辺をn!で割るとうまい具合に進みます。
<筆者の解答>
