東大京大に引き続き、他の旧帝大の問題も取り上げていきます。この記事では、東北大学の2015年の問題を取り上げます。
第1問

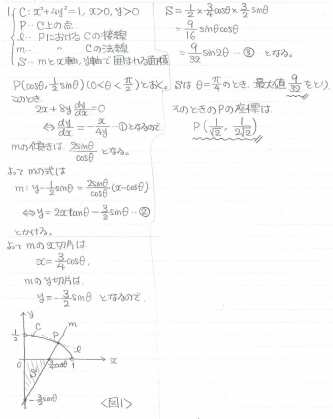
楕円の法線と座標軸が作る直角三角形の面積を考える問題です。
これは、楕円の法線の式がきちんと立てられれば簡単に解ける問題です。
Pの座標を(cosθ、1/2sinθ)として、接線の傾きから法線の傾きを計算しましょう。
<筆者の解答>
第2問

定点から3次関数へ引いた接線が3本になる条件を考える問題です。
(1)は、いきなりDに含まれているPで考えるのはやりずらいので、3本接線を引けるPの範囲がDに収まっていることを証明する、という解き方で行くべきです。
x=tにおける接線がPを通るとき、そんなtが3つ存在する条件を求めましょう。
(2) (1)で考えた3次方程式で、解と係数の関係を使えばよいです。傾きの積が0ということは、接線のうち少なくとも一本はx軸平行です。
<筆者の解答>

第3問

サイコロの目によって決まる2次方程式の解に関する確率の問題です。
2次方程式の判別式の正負を考えることと、解と係数の関係から(2)ではP1 = P3, (3)ではP3 < P1となるものを個別に調べていきましょう。
<筆者の解答>

第4問

極限の問題です。
(1)は、意外と思いつきにくいですが、sinxは固定したままでx^aのみ動かしてみると示せます。
(2) Anの式は簡単に求まるので、(1)の不等式を利用してはさみうちです。
(3)Cnについても(1)と同様の不等式を立て、(2)と同様にはさみうちです。
<筆者の解答>

第5問

鋭角三角形を折り曲げてできる四面体の体積を考える問題です。
(1)鋭角三角形になる条件は、辺の長さをa,b,cとしたときにa^2<b^2 +c^2, b^2<c^2+a^2, c^2<a^2+b^2が全て成立することです。
(2)Hの座標を(t, h)とすることができるので、ベクトルの内積0を使ってhを求めましょう。
(3) 問題文の四面体は全ての面が合同になる、等面四面体になります。等面四面体の体積は、それを含む直方体を作って考えます。
<筆者の解答>


第6問

「k-連続和」について考える整数問題です。
(1)シグマの公式から、n= 1/2k(k+2m-1) と計算できることが出発点です。これから(A), (B)をともに言うことができて、逆も言うことができます。
(2)は(A)をベースに考える方法と、k(k+2m-1) = 2n を利用する方法とが考えられます。結果論、後者の方が楽でした。n= 2^fのとき、kとk+2m-1の偶奇は異なるので、どちらかが1とならないといけないのでk≧2に矛盾します。
前者の場合は、分母と分子に含まれる素因数2の個数を比較することになります。
(3)は、k(k+2m-1) = 2nを利用する方法でないと厳しいです。2×p^fを、偶数と奇数に因数分解する方法を考えます。kとfの偶奇による場合分けが必要です。
<筆者の解答>

