東大京大に引き続き、他の旧帝大の問題も取り上げていきます。この記事では、東北大学の2014年の問題を取り上げます。
第1問

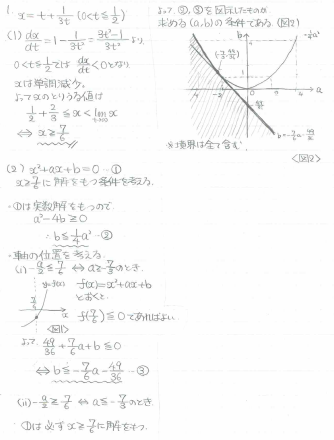
関数の取りうる値と、2次方程式の解の存在条件を求める問題です。
(1)一見すると、相加相乗平均が使える形をしていますが、ひっかけですので騙されないようにしましょう。
なぜかというと、相加相乗平均を使って得られる最小値は、t=1/√3 での値なのですが、1/√3は、0≦t≦1/2に微妙に収まっていないのです。
よって、xをtで微分して、、というオーソドックスな方法でちゃんと調べましょう。
(2)2次関数の軸の位置によって場合分けして考えましょう。
<筆者の解答>
第2問

平行六面体を題材にした問題です。
(1)Nの座標を文字でおいて、MN=4となることからNの座標を確定させます。
(2)E, M, Nを通る平面の方程式を求めてしまうのが近道でしょう。
(3) (2)の結果からPは辺OC上にあるので、考える断面は素直な平行四辺形になります。
<筆者の解答>

第3問

取り出した球の番号の席について考える、確率の問題です。(3)が難しいです。
(1)取り出した球が、2と5の組み合わせならOKです。
(2)100 = 2×2×5×5となるので、4個中2個は5になります。残り2つの積が4となるので、2が2つ、または1と4の組み合わせになります。
(3)n回目に取り出す球の番号をXnとします。
このとき、X1*X2*X3 = X4*X5*X6 となる場合をすべて数え上げます。
簡単なのは、X1~X3とX4~X6が同じ数字の組み合わせのときですが、問題は、異なる数字の組み合わせの時です。
もし、X1~X3がすべて違っていてかつ1か素数の組み合わせだとすると、X1*X2*X3を別の3つの数字の組み合わせの積で表すことができません。よって、X1~X3の少なくとも1つは4になるか、同じ数字を含んでいないといけないことがわかります。
X1~X3に4が入っていないケースのほうが数えやすいので、そちらを数え上げましょう。このとき必然的にX4~X6には4が含まれることになります。
<筆者の解答>


第4問

行列の条件を求める問題です。
これは、Aの形から「回転行列なのでは?」と連想してほしいところです。
A=Oの場合は明らかに不適なので、Aは、必ず回転行列の定数倍の形で書けます。この定数倍が、実は1倍であることを証明しましょう。
1倍以外の場合は、Pか,QとRかの一方はDからはみ出してしまいます。
<筆者の解答>

第5問

積分の計算問題です。
(1) 分子のcosxが、分母のsinxの微分になっていることに着目すれば、置換積分が使えます。
(2)加法定理を使えば、すっきりと計算できる形になります。
(3) (2)の漸化式を何回も使っていきましょう。
<筆者の解答>

第6問

不等式証明の問題です。題材は、n個の数に対する相加相乗平均の関係の特別な場合の証明になります。(2)は発想が難しい難問なので、(1)だけ抑えて(2)は本番では捨ててOKです。
(1)は、式がくどいですが、地道に微分して増減を調べましょう。
(2)は相当な難問です。
(1)の結果から、f(x)≧0がわかるので、この不等式をlogを外して変形していくと、
[ (a+x)/(n+1)]^(n+1) ≧ x (a/n)^n となります。ここから何をすればよいかよくわからないですよね。
これは思いつかなければまず無理だと思うのですが、a=Σ(k+1)/k , x=(n+2)/(n+1)とおくと、求まった不等式は、
(1+1)/1から(n+1)/n までn個の平均 のn乗 = Bn を考えていることがわかります。不等式は、まさにBnの漸化式となっているので、これを何回も使うことによって、
(Bn)^(1/n)= Σ(k+1)/k ÷n ≧ (n+1)^(1/n)というゴール一歩手前まで進められます。
まだ等号が残っていることに注意です。最後は等号成立しないことを示しましょう。
具体的には 左辺が有理数であることに注目して、(n+1)^(1/n)が無理数であることを背理法によって証明します。
これは完璧に捨て問ですね。。。
<筆者の解答>

