私立最難関の一角、慶應義塾大学の医学部の問題を取り上げます。今回は2008年の問題です。
第1問


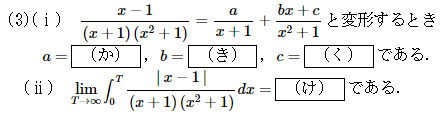
小問集合です。
(1)2円が2点で交わる条件を求める問題です。中心の間の距離が、半径の差より大きく、かつ半径の和より小さければ2点で交わります。
(2)円に内接する三角形の面積の最大値を考える問題です。Pが弦ABのちょうど真上にあれば面積が最大になることが図形的に分かります。この面積の最大値S(r)をrの式で表し、rを動かして増減を調べます。結果として、面積が最大になるのは、正三角形になる時だと分かります。
(3)部分分数分解と、それを利用した積分の計算問題です。
(ⅰ)は分母を払って係数比較すればよく、(ⅱ)は(ⅰ)を使って積分を計算してから極限を計算すればよいでしょう。Tはどうせ無限大に飛ばされる運命なので、最初からT>1として計算してしまってよいです。
<筆者の解答>


第2問


将棋の角のような動きをする点の軌跡を考える確率の問題です。(5)は捨ててしまって問題ない難問です。
(1) 題意を満たすのは、「偶数回目は(0,0)にいる」「奇数回目は(1,1), (1,-1), (-1,1), (-1, -1)のどれかにいる」ときなので、偶奇で場合分けして漸化式を立てましょう。
(2) 状況をよく考えると、点はy=x, y=x-2の2直線のいずれかの上に常にいることが分かります。よって、y=x上にいる確率をan, y=x-2上にいる確率をbnとして漸化式を立てましょう。qn=an+bnです。
(3) (1)を踏まえると、AかつBとなる確率は、「偶数回目は(0,0)にいる」「奇数回目は(1,1), (1,-1), , (-1, -1)のどれかにいる」(※(-1, 1)がNG) 確率となります。
(4) n=3のとき、(a1,b1), (a2,b2), (a3,b3)が全て異なるので、(a1,b1), (a2,b2)はなんでもよく、(a3,b3)≠(a1,b1)となる確率を考えます。
n=4のときは、(a1,b1), (a2,b2)はなんでもよいですが、(a3,b3)=(a1,b1)か(a4,b4)=(a2,b2)のどっちか片方が成立します。
(5)これは難問です。
(a1,b1)と(a2,b2)は常に異なる点なので、3番目の点(X,Y)について考察します。この(X,Y)は、「(a2,b2)から1回で移動できる点」と「(a1,b1)から1回で移動できる点」に大別されるので、(X,Y)が何通り選べるかを各場合について考えます。
<筆者の解答>



第3問

微分方程式の問題です。
(1) 法線の式を計算すれば実質終了です。
(2)△PQRの面積は(1)の結果を使えばf(x)だけの式で書けます。そして、f'(x)>0が成立していれば、この式は簡単にxで積分できます。x=0の条件から積分定数も確定できます。
(3) (1)の結果を同じようにxで積分すると、y^2がxの2次(以下)の式で書けることが分かります。
(4) (3)の結果からf(x)が楕円になる条件が分かり、x軸上に焦点がある時は長軸がx軸になる時です。平方完成を駆使して楕円の式をきれいにすれば、焦点の座標を求めることができます。
<筆者の解答>


第4問

チェビシェフ多項式を題材にした問題です。
(1) これは漸化式を使って愚直に計算して、5次方程式を解きます。とはいえ、この5次方程式は実質2次方程式にできます。最終結果の2重根号は残念ながら簡単にできません。
(2) (1)を解く工程で正直察してしまった人も多いと思います。この問題文の漸化式をみたすn次多項式fn(x)はチェビシェフ多項式と呼ばれ、(2)に書かれている通り、cosのn倍角の公式をつくる多項式になります。証明自体は数学的帰納法で良いでしょう。
(3) (2)の結果からf5(cosθ) = cos5θとなり、θ=π/10のときcos5θ=0なので、cosπ/10はf(x)=0の解の1つになることが分かります。同じように考えると、cos3π/10, cos5π/10=0, cos7π/10, cos9π/10の4つもf(x)=0の解になるので、cosπ/10も含めて5つの解を全てみつけることができました。cosを使わない具体的な形は(1)で求めているので、cosπ/10は(1)の答えの中で最大のものになります。
(4) fn'(x)を計算すればよいのですが、せっかく(2)の関係式があるので、θの微分を絡めてあげるとよいでしょう。ここからfn'(x)=0となるθが求まるので、極値とそのときのxの値を求めることができます。
<筆者の解答>

