理系数学の最難関の一角、東京工業大学の2017年の問題を取り上げます。
第1問

約数について考察する整数問題です。
注目ポイントは 「約数が何個あるか?」 と「どんな素因数が含まれるか」 の大きく2つあります。
(ⅱ)から、12がNの約数、言い換えればNが12の倍数になっていることが分かり、Nは素因数2を2個以上、素因数3を1個以上持っていることが分かります。
ここから、Nが5以上の素因数を持つ場合と、2,3以外に素因数を持たない場合に分けて考えることになります。
前者の場合は、約数が12個という(ⅰ)の制約から、2を2個、3を1個、5以上の素数pを1種類だけ1個もつことが分かります。つまりN=12pと書けます。
この状態で約数を小さい順に書き下して12が何番目に来るかを調べてみましょう。すると、p=5やp≧13の場合はNGで、p=7,11の場合がOKだと分かります。
後者の場合は、(ⅰ)の条件から2の個数と3の個数の候補を絞り込むことができるので、あとは同じように約数を小さい順に書き下して12が何番目に来るかを調べましょう。
<筆者の解答>


第2問
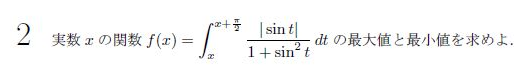
積分で書かれた関数の最大最小を考える問題です。
積分区間の両端にxが入っていてややこしいです。このややこしさを少しでも緩和するために積分の中身を確認してみます。
分子も分母も周期がπの周期関数になっているので、積分の中身全体も周期πになっています。積分が面積だという基本に変えれば、f(x)は積分区間の長さをπ/2に維持したまま横にスライドさせていくイメージとなるので、f(x)それ自体も周期πの周期関数になることが分かります。以上の考察から、xの範囲は0≦x≦πで考えれば十分です。
次に気になるのが絶対値なので、x~x+π/2の間にsintの符号が変わるポイントがあるかないかで状況が変わっています。ということでxの値による場合分けをして絶対値を外しましょう。
ここから積分をいきなり計算してf(x)を積分なしの式で書いて考える、のもアリかもしれませんが、この問題ではf(x)の増減を最優先で知る必要があるので、先にf'(x)を計算する方が得策でしょう。これによってf(x)の増減がわかり、f(π/4)が最大値、f(3π/4)が最小値だと分かります。あとは、積分を計算することで、これらの具体的な値を計算しましょう。
実は、f(x)の積分(で絶対値を取り除いた関数)は、原始関数をきっちり計算することができます。分母をcostの式にしてX=costと置換積分するとうまくいきます。この原始関数をうまく使って、f(π/4)とf(3π/4)を頑張って計算しましょう。
<筆者の解答>


第3問

長方形の折り紙を折った時にはみ出る部分の面積を求める問題です。本番では実際に折り紙が配られたようですが、どんな感じにはみ出るかをイメージさせるための措置でしょう。筆者は、折り紙での実験なしに解きましたが(笑)
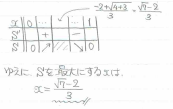
(1)は、xの値による場合分けが煩雑なうえに、面積の計算自体も図形のセンスが必要な難問です。以後、座標xと混同しないようにAP=pとして考え、答案のようにxy座標を置いて考えます。
最初のポイントは、「DがPに重なるように折るという操作は、数学的にどう表現できるか?」を考えることです。これは、「線分DPの垂直2等分線Lについて、折り紙の辺を対称移動をする」と言い換えることができるので、まず考えるべきは線分DPの垂直2等分線Lです。この直線がまさに折り目となります。
この折り目Lが折り紙の各辺とどう交わっているかによって、はみ出す部分の形状が変化するので、Lのx切片とy切片を計算しておくとよいでしょう。これによって、pを場合分けする際の境目の値が分かるわけです。
はみ出す部分は基本的に直角三角形になっているので、斜辺以外の2つの辺がa,pの式で書ければOKなわけで、対称移動をうまく使って合同な直角三角形を作って考えると見通しが良いでしょう。
(2) (1)の結果はxの値によって3種類の関数で書けるわけですが、a=1の場合はラッキーなことに1つの関数に合流します。あとは、これを頑張って微分して増減を調べましょう。
<筆者の解答>

第4問

文字列の場合の数、およびそれに絡んだ確率、条件付確率の問題です。
(1)a~cを使った文字列の総数(つまりAnの個数)が3^n通りあることはすぐに分かるので、(*)を満たす文字列の個数を数えるのがメインの作業になります。直接数え上げるのは難しいので、ここは漸化式の力を借りることにします。
漸化式を立てるポイントは、(*)を満たすn個の文字列を「末尾がcになる文字列」と「末尾がaかbになる文字列」の2種類に分けてn+1文字目にどの文字を追加するかを考えることです。
すると3項間漸化式に帰着できますが、一般項は無理数の混じった複雑な形になります。フィボナッチ数列の一般項を求める作業と類似していますね。
(2) こちらは条件付確率を考える問題です。
計算するには、「7番目がcになる(*)を満たすn個の文字列の個数」と「7番目がcになり、かつ10番目がcになる(*)を満たすn個の文字列の個数」の2つが分かればよく、両者の比がQ(n)となります。
両者を数える際に、(1)の知見を活かすことができます。(1)の解説で「末尾がcになる文字列」と書きましたが、これは「先頭がcになる文字列」でも同じ考え方ができて、
「末尾がcになる文字列の個数」=「先頭がcになる文字列の個数」となります。
最後の極限は、公比の絶対値が1未満になる等比数列をうまく作れれば、その極限を0にできて計算できることになります。
<筆者の解答>


第5問

4次方程式の解が、全て絶対値1の虚数になる条件を考える問題です。
(1) f(x)=0が虚数解さえ持てば、これらの絶対値が1になることはすぐに確かめられます。
(2) F(x)=0の4つの解は、全部が絶対値1の虚数解ならx=cosθ1±isinθ1, cosθ2±isinθ2 の形に書けるので、これらから逆にF(x)の形を、因数分解された形に書くことができます。それを使って2つの2次方程式を作ってしまえばよいでしょう。
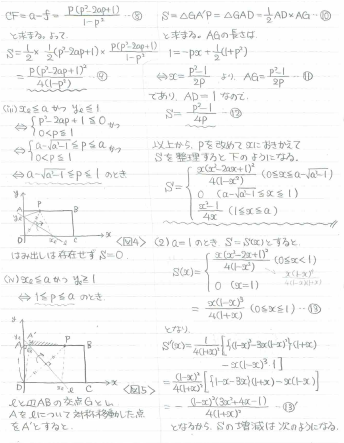
(3) 係数比較からa=c1+c2, b=c1c2 +2 と求まり、(1)から-2<c1<2, -2<c2<2が求まります。このときにa,bがどんな範囲を動くかを考えるのですが、ここで発想が必要になります。
aとbが両方c1,c2の対称式で書けていて、かつ和の形、積の形でそれぞれかけているので、解と係数の関係を使えば、c1,c2は2次方程式t^2 - at + (b-2) = 0の2つの解と解釈できます。よって、この2次方程式の2つの解がともに-2より大きく2よりも小さい実数となるa,bの条件を求めればよいことになります。
<筆者の解答>