このシリーズでは、奈良県立医科大学の後期の数学の問題を解いていきます。
5回目の今回は2018年です。
第1問

確率の問題です。
(1)最初の3回の積が奇数になるのは、3回とも奇数が出る場合なので計算しやすく、積が偶数になる場合は余事象で考えた方がいいでしょう。
あとは、その偶奇で場合分けして、X=10となるようなサイコロの出方を調べればよいです。
(2)後半の議論は(1)と全く同じなので、前半の積の偶奇の確率のみ変わってきます。
<筆者の解答>

第2問

2項係数の最大公約数に関する問題です。
条件を式にすると、n=M×2^r (M:奇数)と書けることがポイントになります。
(1) 与式をうまく変形して、奇数×与式=2n×(別の2項係数)の形に持ち込めば、奇数と2^(r+1)が互いに素なので、与式が2^(r+1)の倍数でないといけないと分かります。
(2)
(1)の結果から、最大公約数は少なくとも2^(r+1)の倍数であり、2nC1=2n=M×2^(r+1)なので、最大公約数は2^(r+1)×(奇数Mの約数)の形に限られます。
この奇数Mの約数が実は1だと言えてしまえばゴールです。
方針としては、2項係数たち全部が3以上の素数pで割り切れないことを背理法で示すことになります。
もし2項係数たちがすべてpで割り切れると仮定すると、これらの和もpで割り切れないとおかしいです。
ところが、2項定理から和を計算すると、2の累乗の形となってpが入る余地がありません。これで矛盾しました。
<筆者の解答>

第3問

正n角形の辺と対角線の長さの2乗の総和を求める問題です。
Cの中心を原点にして、Pkの座標を(cos(2πk/n), sin(2πk/n) )としても一般性を失わず、こうすることによって計算が楽になります。そうすると実質、Σ(定数)と、Σcos{2π(j-i)/n}の2種類の和を計算する問題に帰着します。
前者についてはSの要素の個数を調べればよいだけなので簡単ですが、問題は後者です。
「片方の文字を固定して、もう一方を動かして和を取る」というのが典型解法ですが、今回は三角関数の中に引数が入ってしまっていて、その方法がうまくいきません。
ここは、l=j-iと引数を変換することで見通しが良くなり、lの値に応じてj-i=lとなるような(i,j)の個数を考えればよくなります。
こうして、Σ(n-l)×cos(2πl/n)の形となりますが、これも計算するには発想力が要ります。引数はよく見るとn/2について対称な形になっていて、k=n-lと変換すると、Σk×cos(2πk/n)となります。引数の文字を再びlに戻して和を取ると、
Σ(n-l)×cos(2πl/n)+Σl×cos(2πl/n) = Σn×cos(2πl/n) とΣの中身を簡単にできます。そして左辺の2つのΣは同じ値なので、全体を2で割ることで、
Σ(n-l)×cos(2πl/n) = (n/2)Σcos(2πl/n)
と計算できるわけです。積分計算で時々出てくる「king property」という解法と同じ手法を使っていることになりますね。
そして、Σcos(2πl/n)については、複素数の知識を使うと-1だと計算できます。
ここまでくればもうゴールですね。
<筆者の解答>


第4問

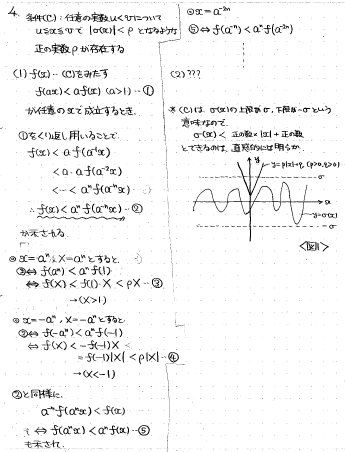
抽象的な関数を不等式評価する問題ですが、この問題に関しては私自身全く解けておりません。申し訳ないです。
(1)の前半の不等式については、f(ax)<af(x)を繰り返し使うことで証明できるのですが、(1)の後半や(2)にあるような「1次関数で上から押さえられる」については、手も足も出ませんでした。
何とか食らいついて、(1)については|x|>1の範囲についてはおおよそ目途が立ちましたが、|x|≦1については上から評価することがついぞできませんでした・・・
ちなみに、(C)は、「σ(x)の上限がρ、下限が-ρに収まっている」という意味になるので、グラフを描いてしまえば、σ(x)が絶対値付き1次関数で上から押さえられることは、直感的には明らかです。それゆえに論証がうまくいかず非常に歯がゆい思いをしてます・・・
<筆者の解答>