このシリーズでは、奈良県立医科大学の後期の数学の問題を解いていきます。
6回目の今回は2017年です。
第1問

微分方程式の問題です。
この手の問題は、両辺をxで微分して簡単にするのが定番ですが、左辺を微分しようとすると、積分区間と非積分関数の両方にxが入っていて、このままでは微分ができません。
ここは、s=x-tと変数変換してあげれば、xを指数関数に押し付けられて積分の外に出せます。こうして積分の外に出たxの指数関数を右辺に追いやることで、両辺をxで微分して積分を解消できる格好にできます。
そうしてあげればf(x)の単純な微分方程式となり、積分定数付きで求まります。元の方程式でx=0としたときの状況を考えることで積分定数も確定できます。
<筆者の解答>
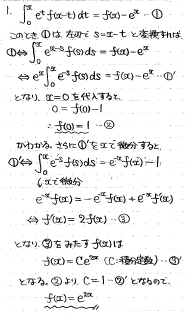
第2問

a+b√2で書ける実数の性質を調べる問題です。背景には、整数の不定方程式の一種である「ペル方程式」があります。
(1) z=a+b√2, w=c+d√2として具体的に計算すればよいでしょう。
(2) (1)の式でw=1/zとすると、右辺が1となります。N(z)は必ず整数になっているので、結局この式は(整数)×(整数)=1 の形になっています。こうであれば、各整数は1の約数になるしかありませんね。
一般に、「x^2 - Dy^2 = ±1 (Dは自然数)」の形の不定方程式のことを「ペル方程式」と呼び、今回求まるx^2 - 2y^2 = ±1は、まさしくペル方程式の1種になっています。
この大問のゴールは、このペル方程式の整数解(x,y)が、±(1+√2)^nを展開したときの係数(√2がない部分がx, ある部分がy)の形に必ずなっていることを証明することです。
(3)発想力が必要です。
単純にz=x+y√2のままだと、xとyの2文字があり、かつ両方ともがプラスにもマイナスにもなりえるので、1<z<1+√2となるx,yの条件が探りにくいです。
ここは1/zをうまく利用することで、xかyの1文字だけの条件にしてしまう事です。具体的には、1<z<1+√2で逆数を取ると√2-1<1/z<1となって、各辺を足すと√2<z+1/z<2+√2となります。これで何が嬉しいかと言えば、(2)の結果から1/zはx-y√2か-x+y√2となるので、z+1/zをするとx,yのどっちかが消えてくれるのです。
全体の流れとしては、1<z<1+√2となるzがあると仮定して、上記の方法でx,yの条件を絞り込み、それが元の不等式と矛盾することを示す、背理法となります。
(4)これまでの検討から、z=±(1+√2)^nが、zと1/zの両方がSに含まれるという性質を満たすこと(十分性)は明らかです。問題は、「この形以外にzが存在しない」という必要性の確認になります。
ここでも発想力が必要で、(3)をうまく利用することにします。
もし、上記の形以外のzが存在する、例えば(1+√2)^n <z< (1+√2)^(n+1)をみたすzが存在すると仮定すると、各辺に(√2-1)^nをかけることで、1<z(√2-1)^n<1+√2とできます。(1)(2)から、z(√2-1)^nも、逆数含めてSに含まれる実数となりますが、これは(3)の事実と矛盾します。
ということで、zを全て探した時、(1+√2)^n と(1+√2)^(n+1)の間には存在しない、つまりzはすべて1+√2のべき乗で書ける、ということになります。
以上はz>0を前提としてましたが、z<0でも全く同様の議論で示せます。
<筆者の解答>


第3問

円周上の点とそれに内接する正n角形の各頂点との距離の積に関する問題です。
これ、L(Q)が最大になるQの位置はおよそ見当が付きます。隣り合った各2頂点を結ぶ円弧の中点だろうと。
この予想が正しいとすれば、正n角形をx軸対称になるように配置すれば、Qは(r,0)にすればL(Q)が最大になることになります(※Cの中心を原点に置いています)。
そうすると、正n角形には、x軸対称となる頂点のペアが複数登場するので、ある特定の頂点のペアA,Bを持ち出して、その時にQA×QBがQ(r,0)のときに最大になることが言えてしまえば、その後は、全てのペアについてその最大値の積を取ってしまえばよさそうです。
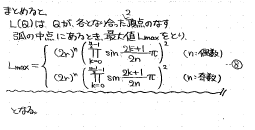
結果、上記の予想が正しいことが分かり、最終的にL(Q)の最大値は、積の記号Πを使った形でnの偶奇で場合分けされた形で表現されることが分かります。
(※nの偶奇の場合分けが発生する理由は、nが奇数の時は、頂点のうちの1つがx軸上に乗って、その点についてだけはペアが作れないからです)
本当なら、最後に残ったΠの形を解消したい所なのですが、その計算方法が分からなかったので、Πを残したままの状態を答えとしました。
(チェビシェフ方程式の利用、あたりもアイデアとしては浮かびましたが、そちらはcosに対しては有効なのですが今回の結果に出てくるsinに対してはあまり有効ではないので・・)
<筆者の解答>

第4問

抽象的な数列の評価に関する問題で、私自身は大雑把な概要レベルの証明(のようなもの)しかできておらず、厳密な証明ができていません。
問題文の条件を解釈すると、「番号がp個進んでも、|an|の値はせいぜい1ずつしか大きくならない」ということになるので、|an|はおおよそ、傾き1/p、y切片|a0|の直線状に増加していくトレンドになります。
そうなれば、αを1より大きく(不安であれば2より大きく)して、βを|a0|より大きくしてしまえば、|an|のトレンド線図よりもαn+βの方が上側に来る、というわけで直感的には題意を説明できたことになります。
が、厳密な証明には何をしたらよいのか、よく分かりませんでした。。。
<筆者の解答>
