このシリーズでは、奈良県立医科大学の後期の数学の問題を解いていきます。
7回目の今回は2016年です。
第1問

格子点の個数を数える問題です。
(1)方針としては、「代数的に計算する方法」と「図形的に計算する方法」の2つがあります。前者は、直線x=k上にある格子点の個数を全て足し上げるというのもの、後者は長方形を対角線で2等分することで数える、というものです。
前者についてはガウス記号が登場することになり少々面倒ですが、高々kは12個しかないので力づくで計算したほうが速かったりします。
後者については、境界線となる対角線にいくつの格子点が載っているかに注意を払う必要があり、これらを足し引きして調整する必要があります。今回の場合は、10と11が互いに素なので、対角線上には端点以外に格子点がありません。
(2)この小問については、後者の「図形的に解く」の方が見通しが良いです。
まず、全体の大きい長方形の格子点数を考え、そこから、欠けている直角三角形の分を差っ引くことでn(S)が計算できます。
ただ、Sは外周も含んでいるので、差っ引く直角三角形は「斜辺を含まない」範囲でないといけません。
aとbの最大公約数dは、この斜辺の上にある格子点の個数を数えるときに必要な情報となります。
<筆者の解答>


第2問

不等式が常に成り立つ条件を考える問題で、今回はガウス記号とよく似ているがなじみの少ない「r以上の最小の整数」が登場しています。
cosxcosyの取りうる値は-1以上1以下なので、不等式の左辺は-1, 0, 1の3つの値のどれかとなることに注意です。
(1)右辺の方の取りうる値は同様にa-1以上a+1以下となります。このとき、(左辺の最大値=1)<(右辺の最小値=a-1)となっていれば、Fが必ず成り立つことが分かります。この時点でa>2の場合はクリアです。
a=2の場合は、左辺が1, 右辺がa-1となっていれば等号成立するのですが、この2つが自同時に実現しないことを確かめていけばよいでしょう。
(2)Fの式を移項すると、a>〇の形にできるので、Oの取りうる値が「2未満」であることが言えれば、題意が示せたことになります。
「cosxcosy」=-1の時は〇=-1, 0のときは〇<1が示せて、「cosxcosy」=1のときはsinxsiny<1 (等号成立しない)となり、かつsinxsinyは1にいくらでも近くできることから、証明が叶います。
<筆者の解答>


第3問

数列の個数を数える問題です。
まず、条件iiのような「項の差がj以上」という条件が考えにくいので、差を具体的に決めてしまいます。ai+1 - ai =j+di (di: 0以上の整数)とおいてしまうと、条件iは、
Σdi ≦ n -(k-1)j -a1と言い換えられます。
a1とd1~dk-1が全部決まれば(a1,・・・,ak)が自動的に決まるので、結局、この不等式を満たすa1とd1~dk-1の組み合わせの個数を調べればよいことが分かります。
流れとしては、
1. Σdi = Nとなる組み合わせの個数を調べる
2. a1を固定した状態でNを0からn -(k-1)j -a1まで動かして1.の結果を足し上げる
3. a1を1からn-(k-1)jまで動かして2.の結果を足し上げる
となります。
1.については、「N個のボールを横一列に並べ、そこにk-2個の仕切りを入れていく」という場合の数の計算方法で調べられ、結果2項係数が登場します。
2.以降ではこの2項係数の和を調べるのですが、残念ながら2項定理が使えない形です。
ここは、「この2項係数をうまく番号が1ズレた差の形に直せないか?」と考えるわけです。これができれば、間が次々に相殺されて最初と最後だけが生き残る形にできます。
ここで使えるのが、「nCk = n-1Ck + n-1Ck-1」という式です。「アイドルグループのメンバーn人からk人を選抜する方法は、『センターを除いたn-1人からk人を選ぶ』+『センターを必ず選んで、残りのn-1人からk-1人を選ぶ』で計算できる」と解釈できる公式です。
この公式を移項することで「番号が1ズレた差の形」にできるので、2, 3,のΣ計算がうまくいきます。
<筆者の解答>

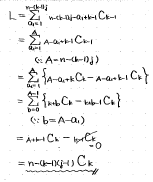
第4問

複素関数に関する、関数方程式の問題です。
(1) Nの式にw=zを代入すると、|f(z)|=|z|が分かります。題意はz=1としたときのこの特別な例ですね。
(2)まず、Nを「Re」を含まない式に直して言い換えることが肝要です。
ただ、このままだと題意がうまく示せません。なぜかというと、Nの式は「Re」を付けることによって「実数だけ」の情報となってしまっているのに対し、証明したい関係式は「複素数の」関係式だからです。だから、Nをいくら弄っても「複素数」としての情報に復元できないのです。
具体的に(a)の例でいうと、Nの式だけでは|f(z+w)|=|f(z)+f(w)|という「絶対値が等しくなる」までの情報しか分からず、ここからf(z+w)=f(z)+f(w)が言えないのです。
では、あくまで「実数だけ」の範囲で「複素数の」等式を証明しようと思ったらどうすればよいか?「差の絶対値が0」が証明できればいいんじゃないでしょうか。具体的には、|α-β|=0→α=β (α,βは複素数)ということです。
というわけで、「差の絶対値が0になる」ことを計算して確かめていきましょう。その際に(1)の結果やNの「Reを取り除いたバージョン」という関係式が役立ちます。
(3) z=a+biとすると、(2)の結果からf(z)=a×f(1) +bf(i)が分かります。あとは、f(i)がうまい具合にf(1)の式で書ければよさそうです。
(2)で考えたNのReなしバージョンの式から、f(1)f(i)* +f(1)* f(i) =0が分かり、両辺にf(1)f(i)をかけてあげると、f(1)^2 + f(i)^2 =0 →f(i) =±if(1)が求まって証明完了です。
(※f(1)は(1)の結果から絶対値1なので、α=f(1)としてしまえばよいわけです)
この部分が発想力が必要でしょうかね。
<筆者の解答>

